Qual dos vetores abaixo forma o maior ângulo com o vetor (1,2,0,2)?
(a) (1,-3,0,2)
(b) (1,1,-3,1)
(c) (1,2,-3,3)
(d) (1,1,1,1)
Passo 1
Vimos que podemos calcular o ângulo entre dois vetores fazendo:
Vamos chamar de v o vetor dado no enunciado
E já calcular a norma desse vetor:
O vetor u vai ser cada vetor das opções. Vamos calcular o valor do para cada um deles e depois ver qual é o maior ângulo.
Passo 2
(a) u = (1,-3,0,2)
Calculando:
Substituindo na fórmula:
Passo 3
(b) u = (1,1,-3,1)
Calculando:
Substituindo na fórmula:
Passo 4
(c) u = (1,2,-3,3)
Calculando:
Substituindo na fórmula:
Passo 5
(c) u = (1,1,1,1)
Calculando:
Substituindo na fórmula:
Passo 6
E agora, como vamos saber qual deles é o maior??
Pra isso, vamos precisar lembrar do círculo trigonométrico!
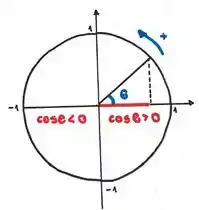
Nele, o valor de um ângulo /2 aumenta conforme o cosseno diminui.
A partir de , o valor do cosseno começa a se tornar mais negativo conforme o ângulo aumenta. Isso ocorre até , quando o ângulo continua a aumentar junto com o cosseno, que vai se tornando mais positivo.
Então, ângulos com cosseno negativo são maiores do que ângulos com cossenos positivos.
A resposta é a letra (a), porque nela encontramos:
Resposta
(a) (1,-3,0,2)