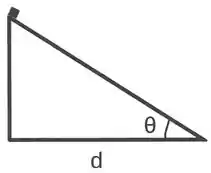
9) Um bloco inicialmente em repouso começa a deslizar do topo de um plano inclinado sem atrito (vide figura). O ângulo do plano inclinado é e sua base tem comprimento d. Se é o tempo que o bloca gasta para chegar à base do plano inclinado, é correto afirmar que:
a)
b)
c)
d)
e)
Passo 1
Fala aí, galerinha! Tudo belezinha com vocês?
Bom, pra gente entender bem direitinho o que está acontecendo, vamos fazer o diagrama do corpo livre para o bloco que está descendo o plano inclinado e sem atrito. Perceba que nessas condições, o bloco descerá desenvolvendo um Movimento Uniformemente Variado, e usaremos essa informação para nos ajudar a descobrir a relação do tempo que o problema está querendo.
Então, boa comigo ver isso acontecendo.
Passo 2
Fazendo o diagrama do corpo livre, teremos:
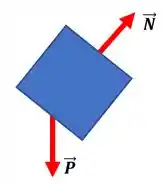
Podemos fazer a decomposição vetorial da força peso em relação ao plano inclinado e teremos:
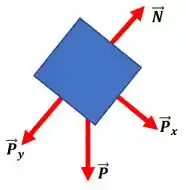
Aplicando a segunda lei de Newton no eixo teremos:
Sendo
Assim:
E poderemos descrever a aceleração do sistema como sendo:
Agora perceba que esse movimento de deslizamento do bloco sobre o plano inclinado é um Movimento Uniformemente Variado , uma vez que a aceleração do bloco varia de maneira uniforme ao longo do deslizamento. Sendo assim, poderemos aplicar as equações horárias do movimento, sendo:
Substituindo que acabamos de encontrar e como o bloco parte do repouso e temos
E a equação se resume a:
Passo 3
Agora perceba que podemos escrever esse em função da distância e do ângulo analisando a geometria do triângulo retângulo.
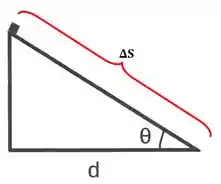
Sendo:
Teremos:
De substituindo na equação horária da posição, ficamos com:
Agora basta isolar o e teremos:
E finalmente, nossa resposta é a letra a)!!!
Prontinho!!
Resposta
Resposta: a)