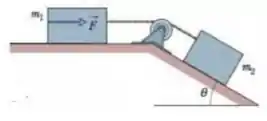
(Capítulo 5.9 – Exercício 66) A Fig. 5-56 mostra uma caixa de massa sobre um plano inclinado sem atrito de ângulo . Ela está ligada por uma corda de massa desprezível a uma caixa de massa sobre uma superfície horizontal sem atrito. A polia não tem atrito e sua massa é desprezível. (a) Se o módulo da força horizontal é , qual é a tensão da corda? (b) Qual é o maior valor que o módulo de pode ter sem que a corda fique frouxa?
Passo 1
E aí galerinha, tudo certoo?
Para iniciar as questões que envolve a segunda lei de Newton, como nesta questão, facilita começar fazendo o diagrama de corpo livre de cada conjunto de bloco:
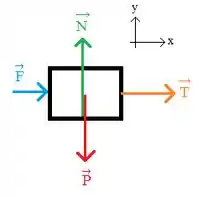
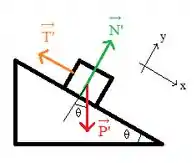
A partir das ilustações acima podemos visualizar melhor as forças que atuam sobre os blocos e, então, escrever a segunda lei de Newton para cada componente.
Passo 2
Temos:
Bloco - eixo :
Bloco 2 – eixo :
Lembrando que como a polia não tem massa e não tem atrito com a corda, ou seja, é uma polia ideal, então o módulo da tração que atua nos blocos são iguais () e como os dois blocos partem juntos, a aceleração do deslocamento é igual para os dois. Show?
Passo 3
a) Portanto, dado o módulo da força , as massas dos blocos e a inclinação do plano inclinado, conseguimos determinar o valor da tração. Para tanto, reescreveremos as equações do passo anterior, já substituindo os valores dados:
Substituindo a na :
Isolando o :
Passo 4
b) Se a corda ficar frouxa, significa que a tração nos blocos será nula, show? Então, para a gente definir o maior valor de precisamos iniciar analisando o bloco para saber qual a aceleração dele quando tende a zero:
Substituindo os valores e isolando o :
Passo 5
Com a aceleração calculada, substituímos este valor na equação do bloco :
E fechouuu
Resposta
- ;
- .