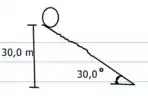
Uma pedra esférica de raio , uniforme e maciça e parte do repouso e rola para baixo de uma colina de 30,0 m de altura e inclinação de , como indica a figura 3. A metade superior da colina é áspera o suficiente para fazer a pedra rolar sem deslizar, mas a metade inferior está coberta de gelo e não há atrito.
a) Calcule a aceleração da pedra na parte áspera.
b) Calcule a velocidade escalar de translação da pedra quando ela atinge a metade da colina.
c) Calcule a velocidade escalar de translação da pedra quando ela atinge a base da colina.
Passo 1
E aí galerinha, como vocês estão por aí?
Oi galerinha, tudo beleza por aí??
a) Nesse problema nós temos um começo e um fim. Interpretando o problema, nós temos um ponto inicial em que a pedra está em repouso e um ponto final onde ela atinge a base da colina. Mas repara que nessa descida ela passa por duas situações diferentes: uma na parte áspera e outra na lisa.
Vamos iniciar resolvendo esse probleminha determinando a aceleração da pedra que é a própria aceleração da gravidade quando decomposta no plano de inclinação de , corresponde a . Considerando que .
Passo 2
Agora destruir o item b em busca da velocidade escalar de translação da pedra quando ela atinge a metade da colina!
Aqui vamos usar o princípio de conservação de energia entre a altura máxima e a metade da sua altura, sendo esse o último ponto onde há força de atrito capaz de fazer a bola girar! Assim, teremos:
Ahh, mas lembra que energia cinética é a soma da energia cinética de translação mais de rotação:
Sendo que cada uma equivale a:
E a nossa energia potencial equivale à metade da altura:
Substituindo esses termos na equação (1), teremos:
Para sairmos essa equaçãozona, temos que aplicar a condição de rolamento que diz que:
Então
Ou sejaaa, temos que a velocidade de translação na metade superior da colina equivale a:
Passo 3
Agora só falta o item c. Aqui nós vamos determinar a velocidade escalar de translação da pedra quando ela atinge a base da colina.
A ideia aqui é usar o famoso princípio da conservação de energia mecânica da metade da rampa até o final !
Como nós determinamos a velocidade inicial, nesse caso, a velocidade que a pedra atinge metade da rampa, temos que:
Organizando os termos, temos que:
Portanto, a velocidade escalar de translação que a pedra atinge a base é:
Prontinho, terminamos ☺
Curtiu a resolução? Responde Aí!!