Qual é o módulo da força horizontal , mostrada na figura abaixo, para o qual o bloco de massa não escorrega para cima nem para baixo sobra a cunha, de massa ? Todas superfícies são livres de atrito.
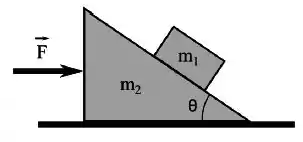
(a)
(b)
(c)
(d)
(e)
Passo 1
Queremos saber a força para que o bloco 1 não deslize na rampa.
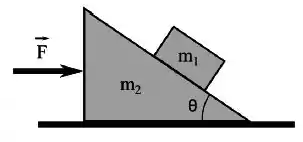
Vamos dar uma olhada nas forças sobre o bloco 1 para entender melhor a situação.
Já decompondo a força peso em suas componentes, temos:
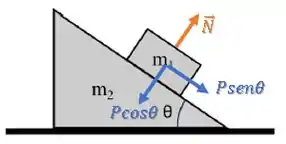
Porém, aquela força aplicada na rampa muda um pouco as coisas.
Primero de tudo, como não temos atrito, a força faz com que tanto o bloco 1 quanto a rampa tenham uma aceleração para a direita.
Porém, quanto maior for essa força , maior será a força normal que a rampa exerce sobre o bloco 1.
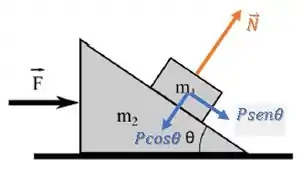
A ideia é que como o bloco 1 não pode estar descendo nem subindo, sua força resultante deve estar na horizontal. Então algum valor de , vai gerar uma força normal que faz o somatório de forças no bloco 1 estar na horizontal.
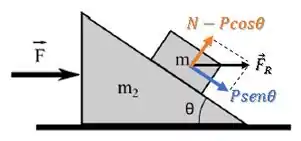
Quando isso acontecer, o bloco 1 terá sua aceleração na horizontal e por isso não subirá nem descerá a rampa.
Passo 2
Então vamos encontrar quem é essa força .
Quando o bloco 1 tiver sua aceleração na horizontal, significa que ele tem a mesma aceleração da rampa. Logo, podemos aplicar a segunda lei de Newton para os dois blocos juntos, considerando que eles sejam apenas um blocão de massa .
Assim, achamos que a aceleração do conjunto em função de é:
Passo 3
Agora, vamos olhar para o bloco 1 para relacionar a força resultante nele com a aceleração.
Como queremos que a aceleração do bloco 1 esteja na horizontal, é conveniente usar os eixos na horizontal e vertical:
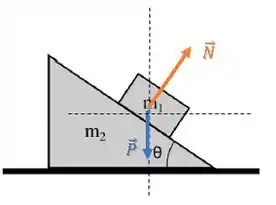
Com um pouquinho de geometria, conseguimos fazer aquele ângulo aparecer ali do lado força normal:
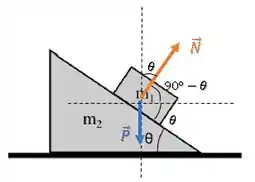
Agora, podemos decompor em suas componentes:
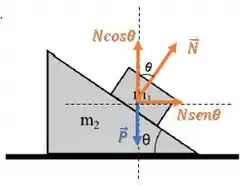
A força resultante no bloco 1 deve estar na horizontal, então a componente vertical de deve se anular com a força :
Então, a força resultante no bloco 1 será apenas a componente horizontal da força :
Vamos juntar essas duas equações dividindo por :
Passo 4
Para terminar, como a aceleração é a mesma no bloco 1 e na rampa, podemos juntar as duas equações substituindo a aceleração.
Ficamos com a alternativa (a).
Resposta
Letra (a)