Um vagão de massa está sobre um plano inclinado de inclinação , ligado a uma esfera suspensa, de massa , pelo sistema de cabos e polias ideais, como ilustrado na figura O coeficiente de atrito cinético entre o vagão e o plano inclinado é e o sistema é solto do repouso.
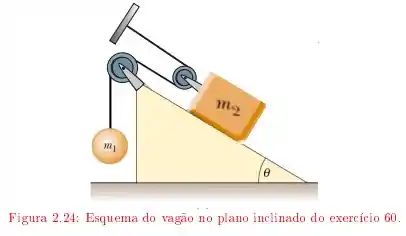
a) Determinar as relações entre os deslocamentos e as velocidades das massas e ;
Passo 1
Fala aí pessoal, tudo beleza?
Nessa questão temos um sistema de blocos, polias e plano inclinado, igual foi mostrado na figura. Basicamente, o bloco ou a esfera irá começar a descer enquanto o outro elemento irá subir. Como eles estão conectados por fio, deve haver um vínculo geométrico relacionando o movimento da esfera e do vagão.
O enunciado nos pede para determinar a relação entre os deslocamentos de e , bem como a relação entre a velocidade deles.

Pra encontrar essa relação é essencial utilizarmos o fato do fio possuir comprimento constante.
Vem com a gente que vamos mostrar todo o procedimento pra encontrar o vínculo geométrico 😊
Passo 2
Vamos começar expressando o comprimento de cada segmento do fio que liga a esfera e o vagão:
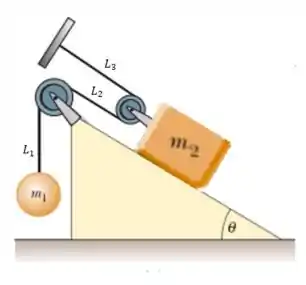
Assim, o comprimento total do fio é dado por:
Agora, vamos imaginar que o vagão desça uma distância no plano inclinado, e que a esfera suba uma distância . Como irão ficar os comprimentos de cada um desses segmentos de fio?
Os segmentos e deverão aumentar em um valor , pois estão conectados ao vagão através da polia móvel.
Já o segmento deverá diminuir de .
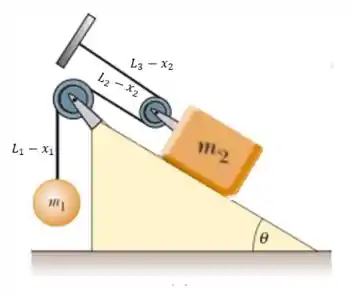
Daí, o comprimento do fio pode ser expresso como:
Como o comprimento do fio é constante, essa expressão deve ser igual à situação inicial. Ou seja:
Logo:
Excelente! Já encontramos a relação entre os deslocamentos da esfera e do vagão. Para encontrarmos a relação entre as velocidades, basta derivarmos a expressão acima com relação ao tempo:
Logo:
Prontinho! Entenderam bem?
Responde Aí!