Um pequeno bloco de massa desliza sobre um plano de inclinação com a horizontal, sem atrito. Sobre ele atuam: a força normal exercida pelo plano e o peso . A opção correta abaixo é:
- O módulo da aceleração do bloco é igual a g.
- O módulo da força resultante sobre o bloco é:
- O módulo da força normal é:
- A aceleração do bloco tem sempre o mesmo sentido da velocidade, independente de qual seja a sua velocidade inicial.
Passo 1
Essa questão é uma questão simples de plano inclinado.
Temos os seguintes dados do enunciado
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Vamos responder as perguntas do passo a passo para colocar as forças no DCL
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Não, não existe mola atuando.
O DCL do bloco fica
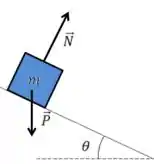
Quando temos um exercício de plano inclinado, é mais fácil considerarmos a horizontal e vertical em relação à superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície. O DCL ficaria
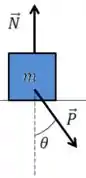
O ângulo fica na força peso com a vertical quando fazemos isso.
Passo 2
No , temos apenas a componente da força peso atuando
Devemos encontrar usando a “regra do COlado, SEparado”.
Passo 3
No temos equilíbrio das forças, tendo
Devemos encontrar usando a “regra do COlado, SEparado”.
Passo 4
Então temos que
Aqui tem uma pegadinha, e você pode ficar em dúvida entre a letra A e a letra C.
Porém, repara que a letra A está escrita em notação vetorial. Isso quer dizer que ela considera que o vetor é proporcional ao vetor , e portanto, eles teriam a mesma direção e sentido, o que é falso. Essa relação seria válida apenas se estivesse escrita levando-se em consideração os módulos dos vetores. Logo, a letra A está incorreta.
Passo 5
Vamos olhar a letra E agora:
“A aceleração do bloco tem sempre o mesmo sentido da velocidade, independente de qual seja a sua velocidade inicial.”
Se a velocidade inicial do bloco é tal que o bloco esteja subindo o plano inclinado a aceleração vai tá querendo fazer o bloco descer, ou seja, no sentido oposto ao da velocidade! Então essa frase está errada também!
Resposta
Letra C