Um carro está dando voltas com velocidade de módulo constante numa estrada curva e inclinada de um ângulo em relação à horizontal. A massa do carro é e o raio da curva é . A velocidade do carro é tal que a força de atrito está atuando no sentido de impedir a derrapagem para cima na estrada. O coeficiente de atrito estático entre os pneus e a estrada de concreto é e o coeficiente de atrito cinético é .
a) Faça o diagrama de corpo livre para o carro nesta situação.
b) Escreva a segunda lei de Newton correspondente na forma vetorial e por componentes nas direções indicadas na figura.
c) Se o ângulo de inclinação da curva com a horizontal for de e se a velocidade do carro for , calcule o valor do módulo da força de atrito estático. Nesta estrada, limite de velocidade é de .
Passo 1
a)
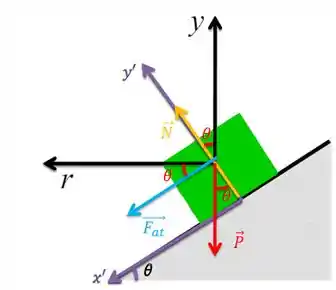
Diagrama de corpo livre é aquele diagrama em que a gente desenha todas as forças que atuam no nosso corpo, nesse caso é o carrinho. Primeira coisa que você faz no seu desenho é transformar o carro em um bloquinho/ponto. E criar um sistema de eixos pra ele, eu chamei de e . Ah, e já esquevi o ali para não esquecer!
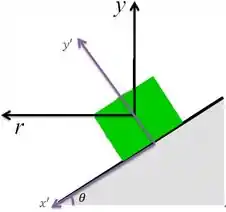
Passo 2
a)
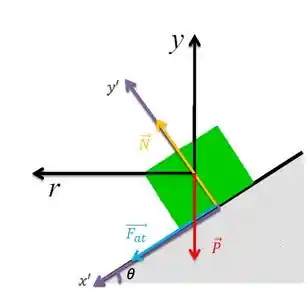
Agora que você já tem seus eixos, vamos marcar as forças:
O corpo está no planeta Terra? Sim! Então tem atração gravitacional tem o peso, apontando pro centro da Terra!!
O corpo está em contato com alguma superfície? Sim! Então tem normal, perpendicular a superfície!!
A superfície é lisa? Não! Ela tem atrito!!(a setinha fica na superfície, mas o sentido dela você tem que analisar! Vamo junto: o atrito é contra o sentido de movimento, lendo lá no enunciado, ele fala pra gente: “derrapagem para cima”, mas eu disse que o atrito é contra o movimento, então a setinha é pra baixo).
Show?
Passo 3
b)
Lembra dos eixos que a gente colocou lá em cima, e do ângulo? Então, agora que eles vão ser úteis! Acompanha comigo:
Vamos decompor todas as forças em componentes que estão na direção r e y! Essas são as direções que o enunciado dá pra gente! E ele pede que a resposta seja dada em relação a esses eixos. Vamos lá então:
O ângulo que a superfície faz com a horizontal é o mesmo ângulo que o peso faz com o eixo , que é o mesmo ângulo que a normal faz com o eixo (ele é um ângulo oposto pelo vértice, isso é um fato da geometria plana). Então fica assim:
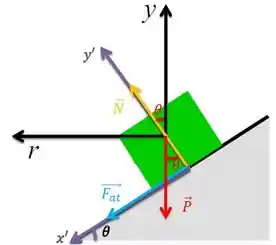
Agora é só ver quem é “colada” e quem está “separada”do . (Lá na teoria de segunda lei tá explicando como fazemos isso!)
Vamos lá.
Passo 4
Aplicando a segunda lei de Newton para cada eixo:
- Primeiro no eixo y, então temos que pegar todas as componentes que estão no eixo y. Entre a normal e o eixo y tem o , então a componente da normal no eixo y é “colada” com com..haha.
- Maravilha, agora vamos fazer para o eixo r:
O peso tá em cima no eixo y, e apontando pra baixo (sinal negativo!), então não precisamos separar em componentes.
A ta longe do eixo y, então vamos colocar ela mais pra cima:
De novo, o que aparece ali é por geometria, lá na teoria tem tudo explicadinho.
Aí a gente vê que a componente da no eixo y está “separada” do
Mas no eixo y não temos movimento, o carrinho não tá pulando pra cima e pra baixo, então a aceleração nesse eixo é zero!
A Normal está “separada” do
A está “colada” no
E quem é a aceleração em r? O carrinho tá fazendo uma curva, então se tem curva, tem uma aceleração para o centro!
Substituindo esse valor:
Prontinho! Sucesso! Já escrevemos a segunda lei nos dois eixos pedidos.
Passo 5
c)
Ele tá querendo o valor da dado um ângulo e uma velocidade
km/h. Essa unidade da velocidade não está no SI,
então temos que mudar pra m/s.
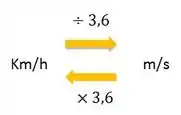
Aí ficamos com: m/s.
Nossos dados são esses daqui:
Agora que tá tudo bonito, vamos usar as equações da letra b pra isolar a :
Dividindo a equação de baixo por e multiplicando por
Somando essa última com a primeira equação, e ajeitando:
Passo 6
Resposta
a)
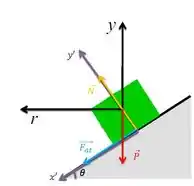
b) Em y:
Em r:
c)