Determine se são verdadeiras ou falsas as seguintes afirmações
Passo 1
Para olharmos se isso é verdade, temos que resolver a inequação e verificar se a solução da conclusão está dentro dela.
Passo 2
Aqui, temos uma inequação modular com “menor que”, então podemos transformá-la em uma única inequação
Podemos resolver essa inequação de forma simultânea
Somando 5 a toda inequação
E essa é a nossa solução
Passo 3
Precisamos resolver essa inequação primeiro para ter a solução rs
isso é uma função de segundo grau.
Vamos começar achando suas raízes
AS raízes vão ser
E
Como , o seu gráfico será algo assim
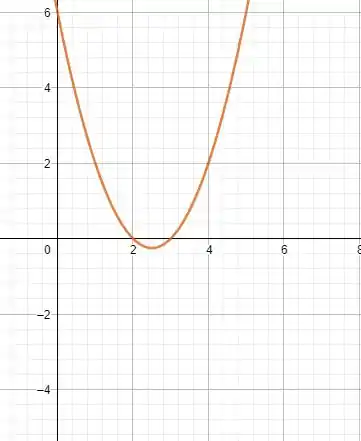
Entre as raízes é negativo e fora é positivo.
Como ele quer a parte positiva, vamos pegar
Isso é
Passo 4
Vamos comparar a solução da inequação com a solução da conclusão
Conclusão
Vimos que a solução da inequação faz parte dela. Então essa afirmação é verdadeira
Resposta
Verdadeiro