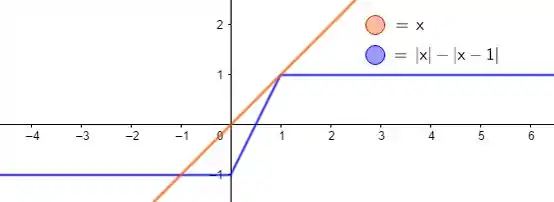
Resolva a desigualdade . Dê o intervalo solução e ilustre a solução sobre a reta real
Passo 1
Opa, vamos lá. Como a gente está trabalhando com módulos, a gente vai acabar precisando estabelecer intervalos. Dá uma olhada no porque:
Veja então que temos 4 condições pra considerar:
E bem, se quisermos escrever em forma de intervalos, podemos fazer assim:
Esses três intervalos de fato levam em consideração as 4 condições acima. Agora é tranquilo, só a gente tirar o módulo da jogada da forma correta, dependendo do intervalo que a gente escolher!
Passo 2
Intervalo
Lembra que funções modulares tem duas leis de formação diferentes dependendo do intervalo? Pois bem, nesse caso aqui, vamos ter que:
Agora é só substituir na inequação:
Passo 3
Intervalo
Nesse intervalo as coisas mudam um pouco, porque vamos ter:
Naaaaada tão diferente aqui galera, vamos seguir a mesma ideia, beleza? Então a inequação fica:
Passo 4
Intervalo
Toda vez que o intervalo muda, pelo menos uma lei de formação muda né! Nesse caso, vamos ter:
A inequação vai ficar então:
Passo 5
Pra fechar com chave de ouro, vamos ver em que intervalos a inequação é verdade. Ou seja, só juntar tudo que achamos nos passos 2, 3 e 4. Saca só:
- no intervalo
- no intervalo
- no intervalo
Sendo assim, o intervalo solução vai ser:
Graficamente, temos:
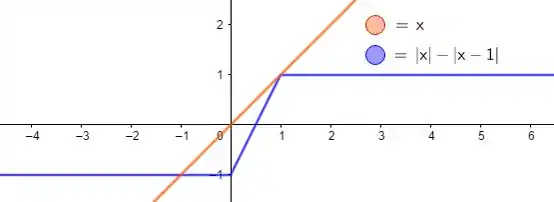
Resposta