Determine a solução da inequação abaixo
Passo 1
Aqui de novo temos uma inequação com módulo, dessa vez é uma função de segundo grau ali dentro, mas não vamos nos preocupar com isso por enquanto.
Vamos entender isso como a inequação módular com menor ou igual, vamos ter duas inequações abaixo
Temos que pegar a interseção das soluções duas inequações.
Passo 2
Vamos começar com a primeira inequação, vamos ter
Arrumando isso vamos ter
Para analisarmos o sinal dessa inequação com função de grau vamos fazer o gráfico dessa função e ver quando ela vai ser menor que .
A função de grau é uma parábola, então vamos ter que achar as raízes primeiro para depois ver como fica o gráfico. As raízes vão ser
Assim temos
O gráfico vai ser
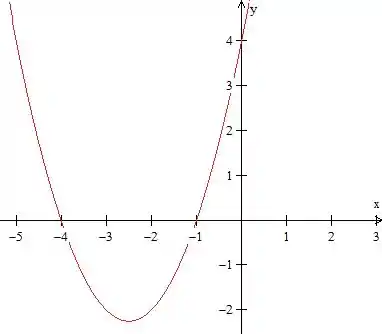
Então a nossa função vai ser negativa entre a e positiva no resto.
Como ele quer a parte negativa a solução dessa nossa inequação vai ser
Passo 3
Vamos começar com a primeira inequação, vamos ter
Arrumando isso vamos ter
Para analisarmos o sinal dessa inequação com função de grau vamos fazer o gráfico dessa função e ver quando ela vai ser menor que .
A função de grau é uma parábola, então vamos ter que achar as raízes primeiro para depois ver como fica o gráfico. As raízes vão ser
As soluções vão ser
O seu gráfico vai ficar
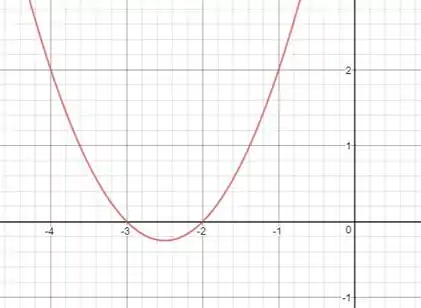
Então a nossa função vai ser negativa entre a e positiva no resto.
Como ele quer a parte positiva da solução dessa nossa inequação vai ser
Passo 4
A nossa solução vai ser a interseção das suas soluções que achamos antes
Assim a interseção dessa parada vai ser