UTFPR - Cálculo 1 - Provas - P1 - 2019.1 - questão 1a
Estude o sinal das expressões abaixo:
Passo 1
Bom dia, boa tarde, boa nooiite gente linda!! Se tá difícil por aí, deixa que a gente te ajuda. Vamos resolver mais uma com muito ânimo e carinho? Bora lá!!
Pessoal a questão quer que falemos sobre como se comporta o sinal da nossa expressão algébrica em relação aos possíveis valores de . Humm, por onde vocês acham que começamos primeiro?
Passo 2
Gente, minha dica é desmembrar a expressão e analisar de início cada parte separadamente e por fim, iremos visualizar como cada uma dessas partes contribui para o todo dentro da expressão. A nossa expressão é a seguinte :
Vamos analisar primeiro essa parte da expressão: , verificamos visualmente que temos uma função modular e que dentro desse módulo temos uma função linear do tipo , certo? Belezinha!
Vamos montar o esboço da nossa função linear:
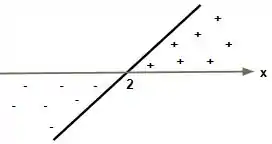
Entretanto temos que lembrar que essa função linear está dentro de uma função modular, logo a imagem da função para esse trecho sempre será .
Passo 3
Agora vamos fazer a mesma coisa para a segunda parte da expressão: . Bom poderíamos fazer o esboço novamente da função linear para essa segunda parte da expressão, porém como temos novamente uma função modular e pelo passo anterior já sabemos que a imagem de uma função modular é maior ou igual a zero. Portanto, como a primeira parte de nossa expressão é positiva e a segunda parte também é, uma vez que o não influencia em nada em relação ao estudo do sinal. Conclui-se o sinal da nossa expressão é POSITIVO para 
.
E aí? Te ajudei? Pois bora terminar de resolver essa prova!
Bons Estudos! :)
Resposta
POSITIVO para ∀x ∈ ℝ.