Determine o domínio da inequação abaixo e seu conjunto-solução
Passo 1
Antes de mais nada vamos entender essa parada de domínio da inequação.
Isso são os valores que a nossa inequação vai dar ruim. Ou seja, a matemática não permite fazer conta.
Como temos uma fração isso vai acontecer quando
Que se torna a seguinte equação
Passo 2
Para resolver essa inequação, primeiro vamos pegar
Resolvendo aquela inequação, vamos ter
E
Resultando em
Assim, temos que resolver a equação para cada intervalo
Passo 3
Com
Esse valor de está no intervalo, então ele é uma as soluções
Passo 4
Com
Esse valor de está no intervalo, então ele é uma as soluções
Assim, vamos ter que o domínio vai ser
Passo 5
Agora, vamos resolver a dita cuja inequação
Mas essa inequação tem dois módulos. Um já abrimos ali em cima. Vamos fazer o mesmo com o outro.
Resolvendo aquela inequação, vamos ter
E
Resultando em
E vamos ter
Passo 6
Temos então intervalos para analisar
Antes do , entre o e o e depois do
Vamos ver como fica a inequação
Organizando as contas
Vamos resolver cada uma dessas inequações e cruzar os resultados.
Passo 7
Temos
Não podemos multiplicar cruzado, devemos passar tudo para a esquerda
Temos que analisar o sinal do numerador e do denominador para colocar no quadro de sinais.
Primeiro o
Ele vai ter raiz em
E o seu gráfico é algo assim
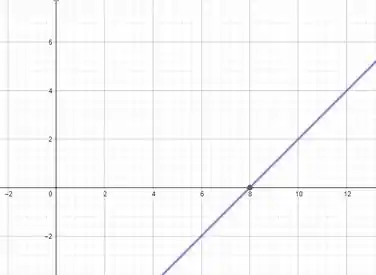
Então antes do ela é negativa e depois é positiva
Passo 8
Vamos agora para o , isso é uma função de segundo grau.
Vamos começar achando suas raízes
AS raízes vão ser
E
Como , o seu gráfico será algo assim
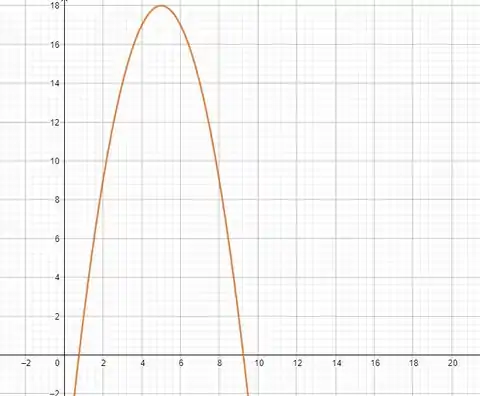
Entre as raízes é positivo e fora é negativo.
Passo 9
Vamos ao quadro de sinais
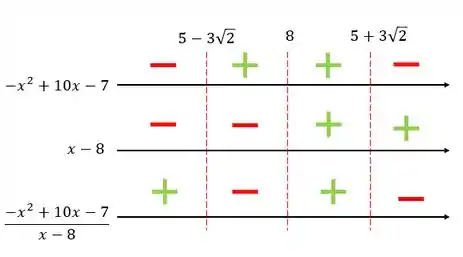
Ele quer a parte positiva, então devemos pegar
Lembrando que no é aberto porque ele está fora do domínio.
Só tem um detalhe importante, estamos trabalhando no intervalo onde
Então, aquele primeiro intervalo não vai entrar, já que é menor que .
Então a solução vai ser
Passo 10
Temos
Não podemos multiplicar cruzado, devemos passar tudo para a esquerda
Temos que analisar o sinal do numerador e do denominador para colocar no quadro de sinais.
Primeiro o
Ele vai ter raiz em
E o seu gráfico é algo assim
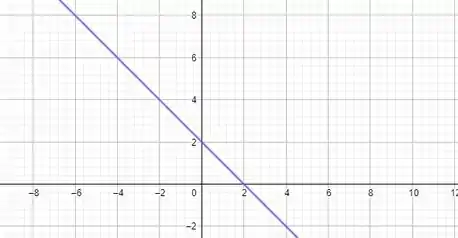
Então antes do ela é positiva e depois é negativa
Passo 11
Vamos agora para o , isso é uma função de segundo grau.
Vamos começar achando suas raízes
Opa, ele não vai ter raiz real. E como o , essa função e sempre positiva. Então só quem vai determinar o sinal é o denominador.
Ele quer a parte positiva, então devemos pegar
Lembrando que no é aberto porque ele está fora do domínio.
Só tem um detalhe importante, estamos trabalhando no intervalo onde
Então não teremos solução nessa parte.
Passo 12
Temos
Não podemos multiplicar cruzado, devemos passar tudo para a esquerda
Temos que analisar o sinal do numerador e do denominador para colocar no quadro de sinais.
Primeiro o
Ele vai ter raiz em
E o seu gráfico é algo assim
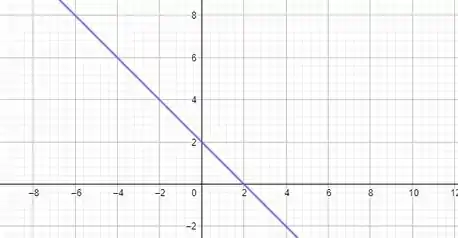
Então antes do ela é positiva e depois é negativa
Passo 13
Vamos agora para o , isso é uma função de segundo grau.
Vamos começar achando suas raízes
AS raízes vão ser
E
Como , o seu gráfico será algo assim
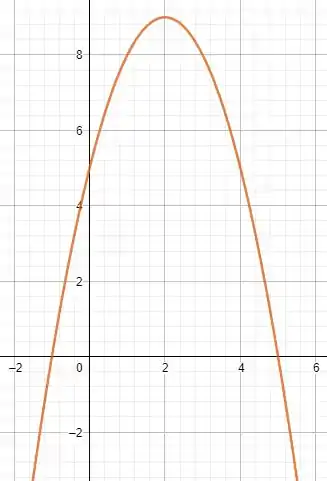
Entre as raízes é positivo e fora é negativo.
Passo 14
Vamos ao quadro de sinais
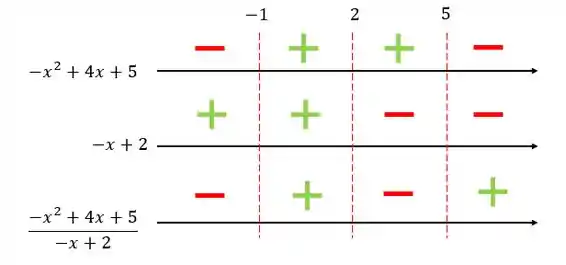
Ele quer a parte positiva, então devemos pegar
Lembrando que no é aberto porque ele está fora do domínio.
Só tem um detalhe importante, estamos trabalhando no intervalo onde
Então, aquele segundo intervalo não vai entrar
Passo 15
Ufa, terminamos as inequações.
Vamos juntar tudo agora
Para juntar basta colocarmos um união
Resposta
Ei, a resposta está no passo a passo :)