Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Triplas em Regiões Gerais

Ver Teoria
Exercício 44123456789101112131415161718192021222324252627282930313233343536373839404142434546474849505152535455565758596061626364656667686970

Enunciado

USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 17c

Calcule

∫ ∫ ∫ D x y d x d y d z , onde D é o tetraedro sólido com vértices ( 0 ,   0 ,   0 ) ,   ( 1 ,   0 ,   0 ) ,   ( 0 ,   2 ,   0 )   e   ( 0 ,   0 ,   3 ) .

Passo 1

Fala pessoal, tudo certinho com vocês? Vamos para mais uma questão de Cálculo. Dessa vez para calcularmos uma integral

Nosso objetivo é calcular ∫ ∫ ∫ D x y d x d y d z , onde D é o tetraedro sólido com vértices ( 0 ,   0 ,   0 ) ,   ( 1 ,   0 ,   0 ) ,   ( 0 ,   2 ,   0 )   e   ( 0 ,   0 ,   3 ) .

Passo 2

Vamos montar nossa integral. Começando pela região D .

∫ ∫ ∫ D x y d x d y d z , onde D é o tetraedro sólido com vértices ( 0 ,   0 ,   0 ) ,   ( 1 ,   0 ,   0 ) ,   ( 0 ,   2 ,   0 )   e   ( 0 ,   0 ,   3 ) .

Vamos desenhar nossa região e sua projeção no plano x y

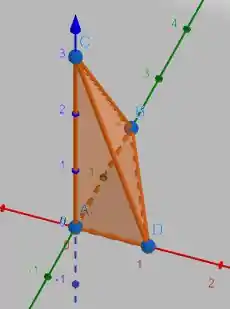
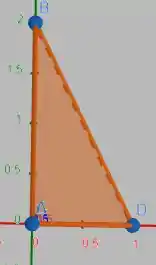
Da projeção, podemos ver que

0 ≤ x ≤ 1

0 ≤ y ≤ 2 - 2 x

Mas e z ? esse é mais complicado. Precisamos descobrir qual é a equação do plano que descreve a face inclinada do tetraedro. Para isso, vamos obter o vetor perpendicular a essa face

Passo 3

Para obtermos essa face, vamos usar Algelin, precisamos encontrar o vetor ortogonal a face e depois construir a equação do plano.

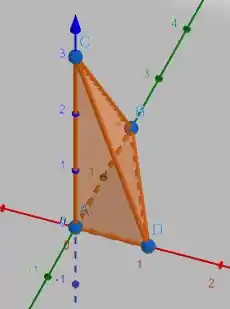
Ao olharmos nosso desenho, podemos observar que os vetores

- ( 0,0 , 3 )   + ( 0,2 , 0 ) = ( 0,2 , - 3 )

- ( 0,0 , 3 ) + ( 1,0 , 0 ) = ( 1,0 , - 3 )

pertencem a nossa face de interesse, e logo pertencerão ao plano que contem essa face. Vamos obter o vetor perpendicular a esses dois, pois este será o vetor normal ao plano

Fazendo o produto vetorial

( 1,0 , - 3 ) × ( 0,2 , - 3 ) = ( 6,3 , 2 )

Logo, sabendo que o plano passa por ( 0,0 , 3 ) podemos construir o plano da seguinte forma

< ( x , y , z - 3 ) , ( 6,3 , 2 ) > = 0

⇒ 6 x + 3 y + 2 z = 6

logo

z = ( 6 - 3 y - 6 x ) / 2

E com isso descobrimos que

0 ≤ z ≤ ( 6 - 3 y - 6 x ) / 2

Passo 4

Agora podemos montar nossa integral. Temos:

∫ ∫ ∫ D x y d x d y d z = ∫ 0 1 ∫ 0 2 - 2 x   ∫ 0 ( 6 - 3 y - 6 x ) / 2 x y d z d y d x

integrando em z

= ∫ 0 1 ∫ 0 2 - 2 x   ( 6 - 3 y - 6 x ) x y / 2 d y d x

= ∫ 0 1 ∫ 0 2 - 2 x   ( 3 x y - 3 y 2 x / 2 - 3 x 2 y ) d y d x

Agora, vamos integrar em y

= ∫ 0 1 ( - 3 / 2   x   ( ( - 1   +   x )   y 2   +   y 3 / 3 )   | y = 2 - 2 x y = 0 d x

= ∫ 0 1 - 2   ( - 1   +   x ) 3   x   d x

integrando, temos que:

= - 2   ( - x 2 / 2   +   x 3   -   ( 3   x 4 ) / 4   +   x 5 / 5 )   | x = 1 x = 0  

= 0.1

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

0.1

Exercícios de Livros Relacionados

Escrever na forma de uma integral tripla iterada: ∫ ∫ ∫ T f d V Onde T é delimitada por x 2 + z 2 = a 2 ,y 2 + z 2 = a 2
Esboçar a região de integração e calcular as integrais ∫ 0 1 ∫ x 2 x ∫ 0 2 + x + y x d z d y d x
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro elíptico 4 x 2 + z 2 = 4 e pelos planos y = 0 e y = z + 2
Calcule a integral iterada. ∫ 0 3 ∫ 0 1 ∫ 0 1 - z 2 z e yd xd zd y
Calcule a integral iterada.int_0^(sqrt(pi)) int_0^x int_0^(x z) x^2 s e n y d y d z d x