- Use uma integral tripla para calcular o volume do sólido limitado por:
- , , , .
Passo 1
Cara! Calculo de volume a esse altura do campeonato pra gente é uma integral tripla de :
Não temos uma boa visualização desse sólido por isso sempre é bom começar por aqui
Relaxa, pois fazer isso nada mais é do que desenhar todas essas superfícies aí ao mesmo tempo! Quando fazemos isso, a superfície que ganhamos no espaço é esta daqui, oh:
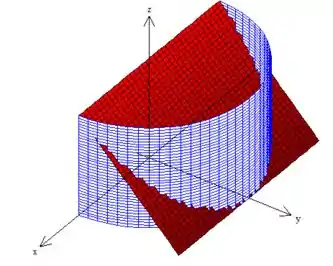
Pegou? :D
Passo 2
Bem, estamos trabalhando dentro de um cilindro, então... Nada mais justo que utilizamos as coordenadas cilíndricas, onde
Não se esquecendo do Jacobiano
Agora, precisamos de encontrar onde essas novas variáveis aí estão variando. Bora? :D
Passo 3
Em relação à ...
o plano vermelho é , então isolando o
trocando pelas coordenadas cilíndricas
Quanto ao e ao , bem, sabemos que eles variam no e no , então olhemos para a projeção do sólido no plano !
Passo 4
Pow, relaxa! Projetar esse sólido nesse plano nada mais é do que olhar para o sólido
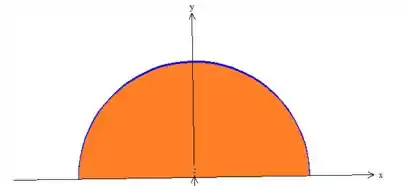
mas dessa vez, de cima para baixo:
O está variando da origem, até o cilindro máximo que é o raio do cilindro azul...
Quanto ao , bem, ele está dando uma meia volta, portanto
Passo 5
Bem, agora é só montar a integral tripla e correr para o abraço!
Substituindo as variações e trocando para coordenadas cilíndricas não se esquecendo de multiplicar pelo ...
Integrando o de dentro e substituindo os limites de integração