Questão 2: Seja
- Obtenha funções , e e uma constante tal que
- Considere a integral tripla
- Fazendo , calcule
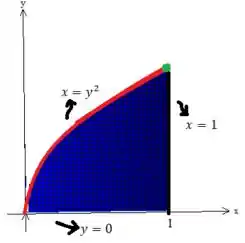
Desenhe a projeção de no plano e explicite no desenho as equações cartesianas das curvas que compõe a fronteira de .
Escreva na forma de uma integral iterada, integrando primeiro com respeito à variável , em seguida com respeito à e finalmente integrando com respeito à .
Passo 1
Bem, se você perceber, essa forma de descrever um sólido, com entre números, entre funções de e entre superfícies em função de e , caracteriza uma descrição de sólido do tipo . E como qualquer descrição, é muito válido a gente fazer uma representação gráfica desse sólido, não acha? Então essa é a nossa primeira tarefa... Desenhar o gráfico de :
Como o próprio enunciado nos disse, é esse cara aqui:
Onde dele, podemos tirar algumas igualdades interessantes:
Essas igualdades representam superfícies quando a gente as desenha no espaço. Por exemplo, as duas primeiras são paredes que esta delimitando o sólido, e essas paredes são planos:
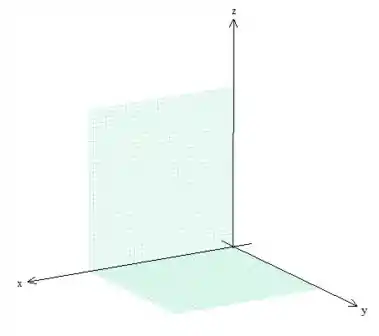
A terceira, caso estivéssemos trabalhando no plano , ela nos representaria uma reta, mas como estamos trabalhando no espaço e, pela equação, independe de , então o plano é paralelo a esse eixo, como se puxássemos essa reta:
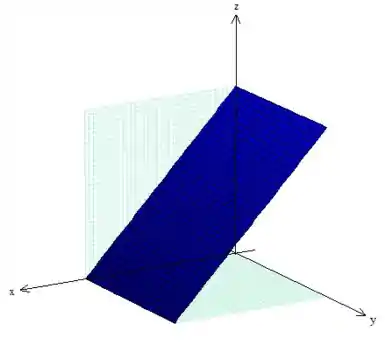
A quarta e última superfície, assim como o plano, se estivéssemos trabalhando no plano , ela seria uma parábola, como estamos no espaço e a equação não possui , isso significa que a o que precisamos fazer é “puxar” essa parábola pra cima de forma que ela faça um cilindro paralelo ao eixo :
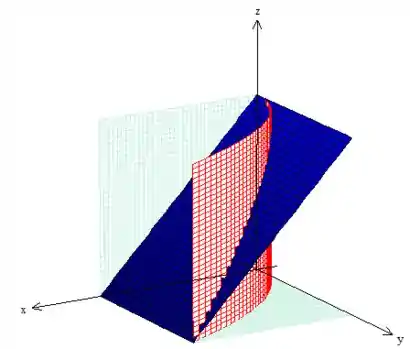
E eis o nosso sólido abaixo desse plano !
Passo 2
Ok, a gente quer descrever a , agora dessa forma aqui:
Veja que o primeiro deles, temos que ter um variando entre superfícies. Se você ver o nosso sólido novamente, podemos pegar o variando da base até o “teto” formado pelo plano azul...
Como o plano azul tem equação...
Logo...
Passo 3
Para a variação de e agora...
É bem legal a gente olhar para a superfície de cima pra baixo, ou seja, para a projeção de no plano :
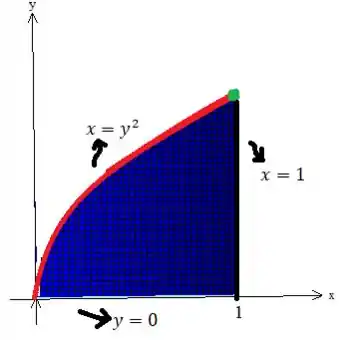
Veja que aí que varia da parábola até essa borda perpendicular:
A parábola tem equação...
Para a borda perpendicular, veja que ela é o encontro do plano com o plano ...
Logo...
Para a variação de , bem, sabemos que ele já varia da reta , até o último valor de que é o ponto de encontro da com a parábola:
Para encontrar a coordenada desse ponto, basta substituir o valor de da reta na equação da parábola:
Logo...
Passo 4
Nesse passo, vamos apenas recapitular o que encontramos, tudo bem? Vimos que o sólido pode ser classificado como do tipo , onde:
Ou seja
Passo 5
Veja que quando esse item do problema nos pede para descrever essa integral aqui
Como...
“... na forma de uma integral iterada, integrando primeiro com respeito à variável , em seguida com respeito à e finalmente integrando com respeito à .”
Veja que para fazer isso, precisamos justamente da região descrita como do TIPO II, afinal se a última integral vai ser com relação à , ele tem que ser o cara que varia entre números! Então aqui não tem muito a fazer, basta substituir as variações de tipo na integral:
Passo 6
Considerando
Integrando com relação a , e portando considerando todas as outras variáveis como constantes...
Continuando a integral, e dessa vez em relação à ...
Calculando essa ultima integral...
Para calcular essa outra integral, podemos fazer uma substituição...
Trocando também as variações de ...
Resposta