Calcule a integral tripla.
Onde é o tetraedro sólido com vértices , , e
Passo 1
Fala aí, galera! Vamos começar essa questão de integral tripla, conhecendo nosso problema. O enunciado nos pediu para fazer a integral tripla:
Mas como ele não nos informou diretamente os limites de integração, então vamos estudar esse volume apresentado:
é o tetraedro sólido com vértices , , e
Colocando isso em forma de gráfico, temos:
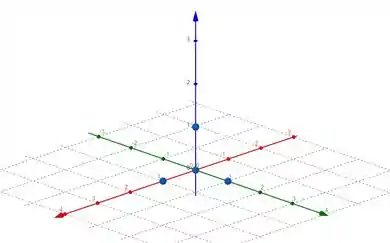
Precisamos achar o plano que passa pelos três pontos que não são a origem, para isso, podemos fazer o seguinte, a fórmula do plano é
Quando e , o valor de . Se substituirmos na fórmula:
Descobrimos que:
Quando e , o valor de . Se substituirmos na fórmula do plano:
Então:
E por fim, quando e , o valor de , então:
Logo o valor de é:
Então temos
Na fórmula do plano, podemos colocar quanquer valor, então para
Logo, a fórmula do plano se torna:
Isolando , temos
Então podemos colocar a variação de como
Passo 2
Agora no plano temos que a área é limitada por , e a reta que passa por e .
Vamos relembrar a equação da reta:
Esse valor é a inclinação da reta, que podemos calcular pelos valores de início e final da reta :
Substituindo os valores, descobrimos que a reta tem inclinação:
Substituindo os valores na equação da reta:
Ficamos com:
Podemos então reescrever o valor de como:
E como em nosso gráfico já vimos que o valor de varia dentro do intervalo de até , temos:
Reunindo todas as informações de intervalos:
Determinamos os intervalos de integração da integral tripla:
Presta bem atenção na ordem de integração, como o valor de depende de e de , então vamos fazer a integração dele primeiro, depois como o valor de varia com o valor de vamos fazer a integração dele e por último, vamos integrar o valor de que tem os limites de integração como valores numéricos!
Show de bola? Então vamos começar as integrações!
Passo 3
Como já falamos antes, vamos começar pela integral em relação a :
Como não temos o valor de dentro da expressão:
Aplicando os limites de integração:
Voltando a nossa integral:
Aplicando a propriedade da distributiva, ficamos com:
Passo 4
Agora calculando a integral dupla:
Vamos integrar em relação a :
Aplicando os valores do intervalo de integração:
Voltamos essa expressão para integral:
Fazendo a substituição dos limites de integração:
Simplificando:
Temos o resultado da integral tripla: