Calcule a integral
Sobre a região .
Passo 1
Vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos uma esfera de raio centrada na origem e um cone, dado pela equação . Repare que, no lugar de onde costumamos ter “”, temos , isso quer dizer que o cone não está centrado em , mas sim em , na verdade, no ponto .
Vamos desenhar isso aí então:
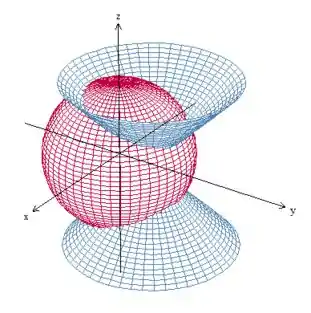
Repare que o problema também diz que . Temos algo assim então:
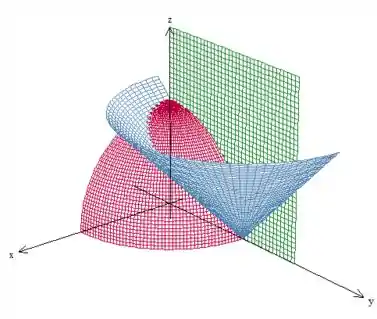
Nossa região é a que está dentro da esfera e acima do cone. Beleza?
Como podemos ver, em o sólido é limitado embaixo pelo cone e em cima pela esfera No plano , temos um domínio , com o qual não vamos nos preocupar por enquanto. Vamos, então, escrever essa região como tipo I:
Passo 2
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 3
Integrando em relação a , temos:
Passo 4
Agora vamos descrever essa região , que é a projeção do sólido no plano . Antes de tudo, temos que fazer a interseção entre essas duas curvas, certo? Descobrir qual é a curva que elas formam no plano . Para isso, precisamos igualar a equação da esfera à do cone:
Agora nós completamos o quadrado do termo , desse jeito:
Quando nós substituímos por , acabamos adicionando à equação um temos que não existia, por isso, tivemos que compensar com um do outro lado.
Não podemos nos esquecer de que !
Bom, isso aí é parte de uma circunferência de raio deslocada da origem, não é? Ela estã centrada em :
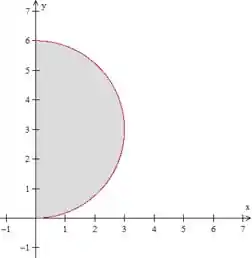
Essa imagem representa o sólido visto de cima, esse é o nosso domínio . Como se trata de uma circunferência, vamos usar coordenadas polares, né? Já que a circunferência está deslocada para , vamos fazer a seguinte substituição polar:
Por que isso? Porque, quando aplicarmos isso à equação esse vai sumir e ela vai se transformar em apenas . É como se estivéssemos trazendo o centro dos novos eixos coordenados para o centro na circunferência. Podemos dizer, então, que (imagine o centro dos eixos coordenados no centro da circunferência).
Não gostou disso? Faz a substituição polar normal então, você só vai encontrar algumas expressões mais trabalhosas, os intervalos de integração serão diferentes, mas está certo do mesmo jeito!
Temos, então, e
Substituindo na integral:
Passo 5
Agora vamos começar integrando em relação a :
Passo 6
Agora em relação a :