Calcule o volume do sólido limitado pelas superfícies de equações , , e .
Passo 1
O volume pedido será dado por . Vamos fazer um esboço dessa região :
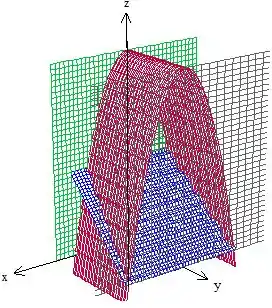
A superfície vermelha representa o cilindro de equação , independente de . Assim, podemos interpretar como várias parábolas ao longo desse eixo. Podemos utilizar o mesmo raciocínio para o plano azul, de equação , independente de .
Como podemos ver a variável varia entre o plano e o cilindro parabólico . No plano , a projeção do sólido representa um domínio . Vamos escrever, então, essa região como tipo I:
Passo 2
Agora precisamos descrever o domínio . Para sabermos que região é essa, vamos fazer a interseção entre o cilindro e plano inclinado:
A projeção da interseção no plano é, portanto, uma parábola de concavidade para cima. Podemos, agora, fazer um esboço dessa região:
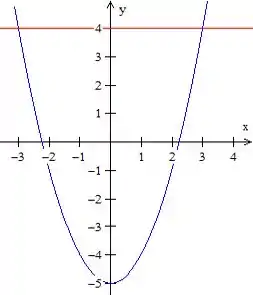
Para descobrirmos a equação dessa reta vermelha basta fazer a interseção do plano inclinado com o plano , ou seja, substituindo em teremos .
Como a região está limitada na esquerda e na direita pela parábola e em cima e embaixo por uma constante, vamos escrevê-la como tipo II. Já sabemos que varia entre e . Isolando os termos na equação da parábola, temos , então, escrevemos a região como:
Passo 3
Vamos agora substituir os intervalos que encontramos para a integral iterada:
Passo 4
Vamos começar integrando em relação a
Passo 5
Agora integraremos em relação a :
Passo 6
Finamente, integramos em relação a :