Questão 4: Seja o sólido dado por
- Esboce .
- Calcule o volume de .
Passo 1
Letra A)
Beleza, retirando as informações de superfícies das inequações do problema:
Agora basta colocar da superfície dessas no espaço:
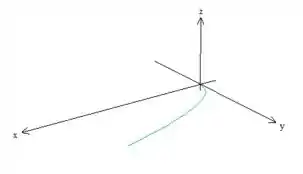
- Vamos começar com . Essa superfície é um cilindro de base parabólica paralela ao eixo :
- , no plano isso é a curva...
- , , e são todos planos:

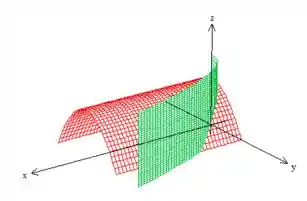
No espaço, basta transladar para cima...
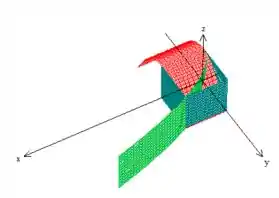
E eis o sólido desenhado !
Passo 2
O volume de um sólido pode ser calculado dessa forma aqui:
Onde deveríamos descrever o sólido e voltar para a integral. Mas por que deveríamos e não temos que fazer isso aqui? Porque ele já está descrito de uma forma que basta substituir na integral !
Temos o variando entre números, o variando entre funções de e o variando entre funções de ...
Bora calcular?
Passo 3
Calculando a integral de dentro...
Agora a do meio...
E a de fora, vamos obter...
Resposta
Letra A)
Letra B)