Encontre a solução geral da equação diferencial dada.

Vamos ver algumas dicas de como resolver uma equação de grau maior que . A ideia é ir achando as raízes aos poucos e ir diminuindo o grau dessa equação.

Quando temos uma equação assim temos alguns candidatos a raízes dessa parada.

Qual o coeficiente do maior grau dessa equação? Neste caso vai ser , vamos chamar isso de

Qual o valor do cara sem a variável ? Vai ser , vamos chamar isso de

As possíveis raízes vão ser os divisores de sobre os divisores de , lembrando que para cada possibilidade vamos ter o cara podendo ser positivo ou negativo.

Os divisores de são e os divisores de são e , assim as possíveis raízes vão ser

Então temos que testar essas duas raízes na equação, como fazemos isso? É só substituir o valor na equação e ver se vai dar , se der o valor de é raiz, se não der ele não é raiz.

Vamos começar testando

Substituindo na equação vamos ter

Como deu , é uma raiz dessa equação. Então vamos ter

Agora que temos uma raiz dessa equação podemos aplicar o método de briot-ruffini para diminuir essa equação em grau. Você lembra como é esse método? Primeiro vamos colocar a nossa equação aqui embaixo

A primeira coisa a fazer é escrever essa equação completa, colocando vezes o elevado aos graus que não aparecem, neste caso a equação já está completa.

Agora montamos o seguinte quadrinho

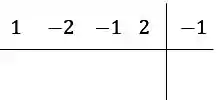
No canto superior esquerdo colocamos os coeficientes da nossa equação, no canto superior direito colocamos o valor na nossa raiz.

Agora nós fazemos os seguintes passos. Primeiro descemos o primeiro coeficiente, que vai ficar

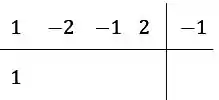
O próximo passo é multiplicar esse número que baixamos pelo número ali no canto superior direito, e depois somar com o próximo coeficiente.

Nesse caso fazemos

Esse primeiro é o coeficiente, o segundo é o número no canto superior direito e aquele é o próximo coeficiente.

Vamos achar , colocamos esse valor embaixo do coeficiente , ficando

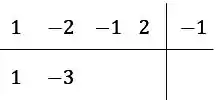
Agora é só repetir, a nossa conta dessa vez vai ficar

E vamos ter

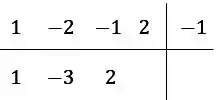
Agora é só repetir, a nossa conta dessa vez vai ficar

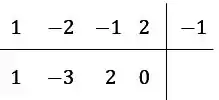
Como aquele último cara deu a nossa conta está certinha, se não der alguma conta está errada.

A nossa nova equação vai ser aquela que tem os coeficientes de baixo, tirando aquele , começando com um grau a menor que o anterior, neste caso vamos ter

Como achamos uma equação de grau podemos fazer como fazemos normalmente. Se essa equação tivesse grau maior que era só fazer tudo que acabamos de fazer de novo para diminuir o grau dessa equação

A nossa equação vai ser

Então temos todas as raízes agora, vamos escrever essas raízes aqui

Beleza agora que temos todas as raízes podemos achar a solução geral dessa EDO.

Todas as nossas raízes tem multiplicidade então nossas soluções vão ser

E a nossa solução geral vai ser

Que vai ficar