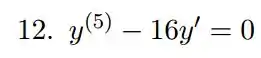
Passo 1
Precisamos resolver a EDO
Encontrando a equação característica
Manipulando um pouco ficamos com
Só aí já encontramos uma das nossas raízes
Passo 2
Para encontrar as outras temos
Que é uma equação biquadrada, fazendo
E encontramos e
Passo 3
Agora precisamos encontrar a solução para cada uma das raízes
Somando as soluções encontramos a solução geral
Resposta
Exercícios de Livros Relacionados
20. y^((4)) - 8 y^' = 0
21. y^((8)) + 8 y^((4)) + 16 y = 0
Em cada um dos problemas de 29 a 36, encontre a solução do problema de valor inicial dado e faça seu gráfico. Como a solução se comporta quando t → ∞ ?29. y ' ' ' + y ' = 0 ;y 0 = 0 , y ' 0 = 1 ,y ' '
Nos problemas 1-36, encontre a solução geral para a equação diferencial dada. y ' ' ' + y ' ' - 2 y = 0
3. Achar a solução geral das seguintes equações diferenciais:a) f ' = 0 ; b) f n = 0 c) f ' = f d) f ' = a fa∈ R .