Resolva o problema de valor inicial
onde
Passo 1
Antes de tudo, precisamos escrever como função degrau, vamos fazer um esboço dela para entender melhor o que está acontecendo.
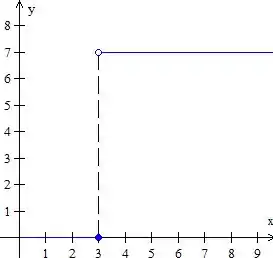
Isso é o mesmo que o seguinte:
Passo 2
Vamos aplicar a Transformada de Laplace à equação.Temos o seguinte:
Aplicando a fórmula
Temos
Agora vamos aplicar aquela propriedade da Transformada da derivada:
Substituindo na equação, temos:
Passo 3
Vamos, então, substituir os valores iniciais e isolar . Temos :.
Isolando :
Passo 4
Certo, agora temos que decompor essa fração:
Em frações parciais.
E seguir o mesmo passo a passo de sempre.
- Fatorar os denominadores
- Igualar a fração à soma de frações com denominadores iguais aos termos que encontramos.
- Fazer o MMC dessas frações, juntá-las ao mesmo denominador.
- Agora, partindo do princípio que essas duas frações são iguais, vamos encontrar os coeficientes das frações parciais.
- Agora que já temos os coeficientes basta reescrever as frações que criamos.
Se você reparar, o denominador não pode ser fatorado, então vamos deixar ele assim mesmo.
O numerador dessas frações que criamos sempre deve ter grau menor que o fator do denominador em uma unidade, como tem grau 2, seu numerador tem grau 1
Vamos juntar os termos pelos graus de .
Como os denominadores já são os mesmos, temos
Vamos agora igualar cada coeficiente das potências de na esquerda e na direita. Como assim? Olha só:
Levando isso para nossa expressão de , temos:
Passo 5
Agora vamos dar atenção ao denominador
Olhando para issos, não parece nenhuma transformada conhecida, mas se tivesse só nós pensaríamos em um seno ou cosseno, não é? Vamos então fazer um pequeno algebrismo aqui para reconhecer esse seno.
Sempre que você encontrar um denominador desse tipo, você deve completar o quadrado do polinômio. Como assim? Vamos agrupar os termos que tem “” em um quadrado perfeito, olha só
Isso nos dá
Passo 6
Precisamos, finalmente, reconhecer a função. Calma, tá acabando! Vamos separar mais essas frações:
Vamos fazer aparecer um no numerador da última fração Ivocê já vai entender porque):
Repara o seguinte:
A mesma coisa acontece para o cosseno!
Vamos substituir isso e:
Agora nós temos 2 problemas: essas transformadas em e essa exponencial que sobrou do lado de fora.
Para trazer a transformada para , vamos usar a seguinte fórmula:
Ou seja, só precisamos multiplicar o que está dentro de por :
Para resolver o problema da exponencial do lado de fora, precisamos dessa fórmula aqui:
Temos então
Logo