UFABC – Fenômenos Mecânicos – Lista 5 – Questão 06
Amplificador de velocidade. Na figura, o bloco 1, de massa , desliza ao longo de um eixo em um piso sem atrito, com uma velocidade , até sofrer uma colisão elástica unidimensional com o bloco 2, de massa , inicialmente em repouso. Em seguida, o bloco 2 sofre uma colisão elástica unidimensional com o bloco 3 de massa , inicialmente em repouso.
- Qual é a velocidade final do bloco 3?
Comparados aos valores iniciais do bloco 1,
(b) A velocidade,
(c) a energia cinética e
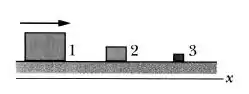(d), o momento do bloco 3 são maiores, menores ou iguais?
Passo 1
Oi pessoal, tudo bem? Essa é uma questão que parece complicada, mas vou ajudar você a decifrar! Temos duas colisões em sequência: primeiro o bloco 1 se choca com o bloco 2 (que está em repouso inicialmente), e ambos adquirem velocidade. Depois o bloco 2 se choca com o bloco 3 (que também estava em repouso), e agora todos os blocos estão em movimento
E note que as massas dos blocos vão sendo cada vez menores, isso indica que eles adquirirão uma velocidade maior após a colisão. Por isso o nome do problema é amplificador de velocidades
Ele é definido como a razão entre o módulo da velocidade relativa de afastamento e o módulo da velocidade relativa de aproximação, assim:
E quando a colisão é elástica, que é nosso caso! Então é isso, vamos usar conservação de momento linear e o coeficiente de restituição para calcular as velocidades finais
Mas relaxa, vou fazer passo a passo contigo! Vamos começar?
Passo 2
Letra (a): Vou começar chamando de e como , então .
Na primeira colisão temos apenas os blocos 1 e 2 envolvidos
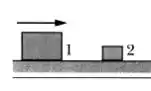
O bloco 1 se move com velocidade de e o bloco 2 está em repouso . Depois da colisão, ambos estão em movimento, assim pela conservação do momento total:
Dividindo tudo por e multiplicando por 2:
Beleza?
Como a colisão foi elástica, então o coeficiente de restituição é 1
Ele é definido como a razão entre o módulo da velocidade relativa de afastamento e o módulo da velocidade relativa de aproximação, assim:
Como e temos
Juntando essas duas equações vamos obter os valores das velocidades depois da colisão:
Partiu resolver esse sistema!
Passo 3
Ficamos com um sistema e você pode resolver da maneira que quiser! Eu vou substituir da segunda equação para achar :
E agora podemos usar qualquer uma das duas equações para descobrir , vou usar a segunda:
Tranquilo até aqui?
Agora o bloco 2 vai em direção ao bloco 3. Aqui vai começar nossa segunda colisão!
Passo 4
Para segunda colisão, o bloco 3 está inicialmente em repouso e tem massa metade da massa do bloco 2, então . E a velocidade inicial do bloco 2 é a velocidade que ele adquiriu da colisão com o bloco 1, que chamamos de no passo anterior!
Assim, para essa segunda colisão
Aí pela conservação do momento linear:
E fazendo o mmc temos a primeira equação:
Vamos guardar essa equação!
A colisão foi também elástica então o coeficiente de restituição é 1:
E essa é a segunda equação! Agora ficamos com esse sistema:
Bora resolver?
Passo 5
Vou substituir a segunda equação na primeira:
Essa é a velocidade final do bloco 3!
Passo 6
Letra (b): agora o problema pede para compararmos a velocidade inicial do bloco 1 com a velocidade final do bloco 3
A velocidade inicial do bloco 1 era:
A velocidade final do bloco 3 era:
Logo, a velocidade é maior no bloco 3 do que no bloco 1
Passo 7
Letra (c): o problema pede para compararmos a energia cinética inicial do bloco 1 com a energia cinética final do bloco 3
A energia cinética do bloco 1:
A energia cinética final do bloco 3:
Assim, a energia cinética é menor no bloco 3 do que no bloco 1
Vamos para a última comparação!
Passo 8
Letra (d): o problema pede para compararmos o momento linear inicial do bloco 1 com o momento linear final do bloco 3
O momento linear do bloco 1:
Momento linear final do bloco 3:
Assim, o momento linear final do bloco 3 é menor do que do bloco 1.
Ufa! Agora sim terminamos!
Espero ter ajudado!