Dois pêndulos de comprimento estão suspensos juntos conforme a figura abaixo. O pêndulo (de massa ) é solto a partir do repouso de uma altura enquanto que o pêndulo (de massa ) está em repouso na posição vertical.
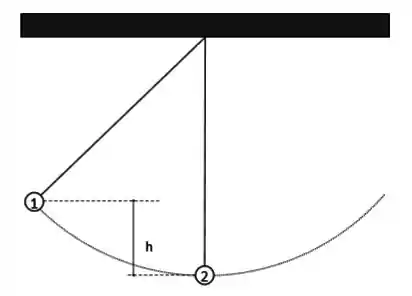
Considerando inicialmente que a colisão é elástica determine:
A velocidade do pêndulo imediatamente antes do choque.
A velocidade de cada pêndulo imediatamente depois do choque.
Dado: .
Passo 1
Por conservação de energia:
Tomando o ponto mais baixo como referencial de energia potencial nula, e lembrando que o pendulo parte do repouso, portanto :
Passo 2
Visto que o enunciado informou para tratarmos como uma colisão elástica, ou seja, sem perdas de energia. Podemos utilizar conservação de energia cinética e conservação de momento linear.
Por conservação de momento linear:
O Pendulo estava em repouso antes da colisão, portanto .
Por conservação de energia cinética:
Novamente, lembremos que
Ficamos então com o sistema:
Substituindo a primeira equação na segunda temos:
Substituindo agora o na primeira equação do sistema:
Substituindo agora que , e .
Lembrando que:
Resposta