Uma partícula (1) de massa se move na direção positiva do eixo com velocidade no topo de uma mesa sem atrito de altura . Ao final da mesa encontra-se uma partícula (2) de massa . Ignore a dimensão das partículas.
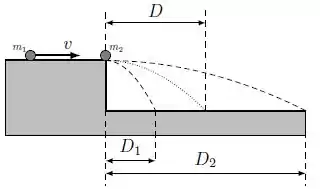
a) Supondo que a partícula (1) colide com a partícula (2) elasticamente como é descrito na figura, encontre a distância total percorrida por cada partícula em relação a base da mesa (na figura as distâncias são representadas por e , suas trajetórias são descritas pelas linhas tracejadas). O tempo de queda é .
Passo 1
Essa questão se divide em duas partes.
A primeira delas é uma Colisão Elástica, onde vamos encontrar as velocidades finais de cada partícula.
Feito isso, vamos à segunda parte que é um Lançamento Horizontal a partir da mesa, onde nosso objetivo será achar o alcance de cada partícula.
Passo 2
Começando pela colisão...
Já durante a colisão não há ação de forças externas (peso e normal se anulam), o momento linear do sistema vai se conservar:
Além disso, como a colisão é elástica, a energia cinética do sistema também se conserva:
A partir dessas duas equações, conseguimos encontrar as velocidades das partículas.
Passo 3
Inicialmente, apenas a partícula (1) se move, portanto ela é a única com momento linear:
A massa e a velocidade inicial da partícula (1) é :
Já após a colisão, temos movimento das duas partículas, então consideramos o momento linear de ambas:
Substituindo as massas:
Passo 4
Já temos o momento linear inicial e final . Podemos jogar na equação da conservação do momento linear:
Achamos a primeira relação entre as velocidades.
Agora, vamos utilizar a energia cinética para a segunda relação.
Passo 5
Novamente, como no início apenas a partícula (1) se move e após a colisão as duas partículas se movem, a conservação da energia cinética ficará:
Substituindo as massas e e também o valor da velocidade inicial de (1) :
Achamos nossa segunda relação.
Passo 6
Ficamos com esse sistema:
Substituindo o valor de da primeira equação na segunda, temos:
Agora, temos uma equação do segundo grau e queremos achar as raízes.
Se simplificarmos todos os termos por uma constante, as raízes serão as mesmas, então vamos dividir por :
Aplicando o Bháskara, temos:
Achando as raízes:
O primeiro valor para será:
E o segundo valor para será:
Mas como sabemos qual deles está correto?
Precisamos aplicar os dois valores na equação para achar e ver qual deles é fisicamente coerente.
Passo 7
Vamos achar o valor de a partir da primeira equação, que é mais simples:
Aplicando :
Pensa comigo, numa colisão unidimensional, se a partícula (1) que estava andando para a direita bate na partícula (2) parada, porém a partícula (2) continua parada enquanto a partícula (1) sai com a mesma velocidade.
Isso é incoerente!
Então, o valor correto será o outro que achamos.
Aplicando :
Passo 8
Agora, achamos as velocidades finais de cada partícula:
Vamos usar esses valores na segunda parte do nosso problema, o Lançamento Horizontal.
Normalmente, temos que trabalhar primeiro o movimento vertical para encontrar o tempo de queda e depois achar o quanto a partícula andou na vertical ao longo desse tempo.
Porém, a questão facilitou para a gente e já nos deu o tempo de queda ().
Como na horizontal, as partículas realizam um movimento uniforma (velocidade constante), basta aplicarmos esse valor de tempo na equação de movimento de um :
Para a partícula (1), temos:
Já para a partícula (2), temos:
Resposta
(a)