Uma bolinha de massa e velocidade colide com outra bolinha de massa (inicialmente em repouso) como mostra a figura abaixo. Considere que o choque é elástico (a energia mecânica se conserva) e que .
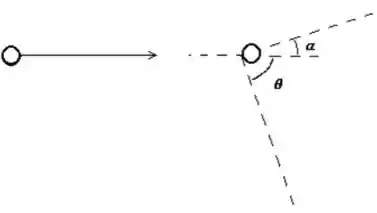
Escreva as equações de conservação de e de .
Calcule as velocidades finais.
Passo 1
Quando temos uma colisão elástica, temos que a energia mecânica total do sistema se conserva. No caso do nosso sistema, onde temos duas bolinhas, a equação da conservação da energia mecânica será:
Sabendo que as massas são iguais, e que , temos:
Passo 2
Pela figura, podemos perceber que se trata de uma colisão em duas dimensões, quando isso ocorre, podemos tratar cada coordenada separadamente. Para o momento linear, ou quantidade de movimento, temos:
No eixo :
sabendo que as massas são iguais, e , temos:
No eixo :
sabendo que as massas são iguais, e que , temos:
Agora que temos todas as equações, vamos para a letra !
Passo 3
Para determinar a velocidade final das bolinhas temos que lembrar da relação entre o módulo das velocidades e suas componentes, pela regra do “COlado/SEparado”
sabendo da relação , temos:
Agora que temos as componentes da velocidade final da bolinha em função do módulo da velocidade, podemos agora achar a mesma relação só que para a bolinha !
Passo 4
Pela conservação do momento linear no eixo , temos:
ou seja:
Pela conservação do momento linear no eixo , temos:
Substituindo , temos:
Agora que temos todas as componentes em função do módulo da velocidade final da bolinha , é só substituir na equação da conservação da energia mecânica, se liga no próximo passo!
Passo 5
Pela equação da conservação da energia mecânica, temos:
substituindo os valores em função de :
Substituindo na equação na energia mecânica, podemos determinar a velocidade da bolinha !
Resposta
Conservação da Energia Mecânica:
Conservação do Momento Linear:
;