Uma bola de massa é presa a um pino por um fio leve e inextensível de 0,8 m de
comprimento. A bola é abandonada quando o fio está na horizontal. Na parte mais baixa da sua trajetória, a bola atinge um bloco de massa , inicialmente em repouso sobre uma superfície áspera. A colisao entre eles pode ser considerada perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é . Considere a aceleração gravitacional .
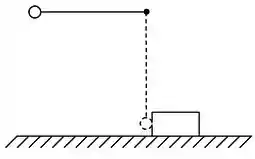
- Qual é o trabalho realizado por cada força atuando sobre a bola até o momento logo antes da colisão?
- Qual é a velocidade de cada corpo depois da colisão?
- Até que altura sobe a bola após a colisão?
- Qual é o trabalho realizado pela força de atrito sobre o bloco até parar?
- Qual é a distância percorrida pelo bloco?
Passo 1
Questão que abrange vários temas da Física I, então é essencial estar com todos os conceitos na ponta do lápis para resolver. Simbora!!!
O problema nos fornece os seguinte dados:
Passo 2
a)
Primeiro devemos identificar cada força que atua no sistema. Isolando essas forças, temos que:
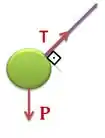
Passo 3
Tá, temos a tração e a força peso! Nesse caso, a tração está sempre perpendicular ao movimento e assim o trabalho da tração será nulo.
Já o trabalho da força peso, depende só da diferença de altura e podemos calculá-lo por:
Como no final a bola vai estar rente ao chão e a corda vai estar toda esticada, nosso será .
Mas por que o sinal de menos?
Porque a bola está descendo, assim a variação de altura será negativa.
Agora sim, calculando o trabalho, teremos:
Passo 4
b)
Como a colisão é perfeitamente elástica sabemos que o momento se conservará e a energia cinética também. Em outras palavras...
and
Sabemos que e .
Como inicialmente o bloco está parado, podemos dizer que , e assim a nossa primeira relação seria:
Pela conservação da Energia Cinética, teremos que:
Passo 5
Dessas incógnitas aí quem a gente já sabe?
Sabemos que m, M e podemos descobrir o da seguinte forma:
Sabemos que a bola foi solta com velocidade quando o fio estava na horizontal. Ao chegar no chão, logo antes de tocar o bloco, toda a energia potencial gravitacional armazenada na bola se transformará em cinética e , pela conservação da energia mecânica, a gente vai ter:
Nos restaram duas incógnitas e duas equações. Tá lindo! Agora é só resolver o sistema.
Passo 6
“Ajeitando” a equação C e B, vai ficar:
Na B:
E na C:
Passo 7
Dividindo C por B:
Só lembrando que
E a partir daí a gente acha que:
Passo 8
Agora pegando aquela equação B e substuindo os valores conhecidos de e acabamos com o problema!! :D
Como a gente já sabe que , substituindo o valor que a gente acabou de achar, teremos...
O que isso nos diz?
A bola vai voltar com a velocidade de e a caixa irá para frente com .
Passo 9
c)
Opa! Como acabamos de ver no fim na b a bola vai voltar com velocidade de 2,4m/s. Lembra daquele primeira relação que a gente achou no Passo 5? É, também vai ser válida aqui.
Passo 10
d)
Bora pensar um pouco! A gente já viu que o bloco vai com uma velocidade pra frente de 1,6m/s. Beleza, se ele tem velocidade tem energia cinética, ok? Mas se ele vai parar, a velocidade será zero e a energia cinética também.
Daí a gente pensa:“o que faz o bloco parar?” . E a resposta é: “Tá na cara que é a força de atrito”.
Pois bem, essa força de atrito realiza um trabalho para diminuir a velocidade, ou melhor, para reduzir a energia cinética. Toda a energia cinética perdida será dissipada pelo trabalho da força atrito, assim podemos reescrever essa relação que a gente acabou de achar como:
Passo 11
e)
Como acabamos de ver, o trabalho da força de atrito tem módulo de 2,56J. Sabemos que o trabalho pode ser calculado por , sendo justamente o que a gente quer e essa F aí é a força de atrito dada por:
Assim, substituindo na fórmula do trabalho vai sobrar:
THE END! :D
Resposta
- ,