USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 59c
Um bloco de massa deslizando sobre uma mesa horizontal, com coeficiente de atrito cinético colide com uma mola de massa desprezível, de constante de mola inicialmente na posição relaxada. O bloco atinge a mola com velocidade de .
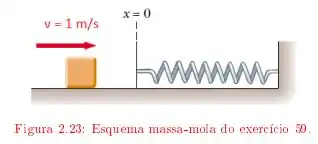
c) Que fração da energia inicial é dissipada pelo atrito nesse processo?
Passo 1
Faaala gente bonita, como vocês estão?
Aqui temos um bloco que atinge uma mola , inicialmente relaxada, com velocidade de . Na superfície horizontal em que a mola se encontra, tem um atrito de .
Vimos nos itens anteriores que ao atingir a mola a energia cinética inicial do bloquinho vai sendo dissipada pelo atrito e transformada em energia potencial elástica.
Encontramos que a deformação máxima da mola vale:
Lembrando também que, como o a força de atrito é constante, o trabalho realizo por ela vale:
Tranquilo?
Então vamos lá, botar a mão na massa!
Passo 2
Para calcularmos a energia dissipada através do atrito até o momento em que a mola tem sua compressão máxima, basta usarmos que:
Assim:
Já a energia mecânica inicial era toda de energia cinética, logo:
Logo:
Portanto, agora basta calcularmos a fração de energia dissipada fazendo:
Logo:
Portanto, aproximadamente de energia mecânica foi dissipada durante o processo.
Prontinho pessoal, curtiram a solução?
Responde Aí!