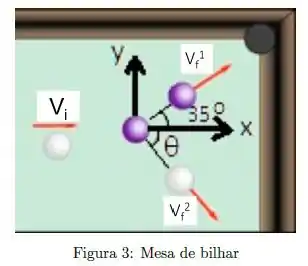
Num jogo de bilhar, um jogador deseja colocar a bola roxa/escura na caçapa, como mostrado na figura. Se o ângulo da caçapa é , em que ângulo a bola branca é defletida? Considere que a colisão é elástica e despreze o atrito e o movimento de rotação das bolas, e considere bolas de massas iguais.
(A) .
(B) 50.
(C) .
(D) .
(E) .
Passo 1
Temos uma colisão bidimensional.
O primeiro ponto importante é que estamos desprezando o atrito e a rotação das bolas. Isso somado ao fato de que as forças externas (peso e normal) se anulam permite que a gente trabalhe esse problema como uma colisão isolada, como fazemos normalmente.
Assim, podemos dizer que o momento linear do sistema se conserva:
O segundo ponto importante é que temos uma colisão elástica, isso significa que além do momento linear se conservar, a energia cinética se conserva também:
Agora, vamos ao problema...
Queremos a direção (ângulo) da velocidade final da bola branca . Então, vamos escrever as equações de momento linear e de energia cinética para determinar as componentes dessa velocidade final.
Passo 2
Vamos começar com o momento linear.
O momento linear do sistema é um vetor, porém, podemos analisar cada eixo separadamente, logo temos:
Vamos decompor as velocidades finais nas componentes horizontal e vertical:
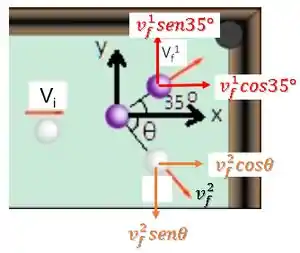
No eixo , temos:
Enquanto no eixo , temos:
Passo 3
Agora, vamos escrever a equação das energias cinéticas:
Cortando as massas e os “2”:
Passo 4
Assim, ficamos com o seguinte sisteminha:
Esse sistema é um pouco chatinho de resolver, mas tem uma coisa que ajuda muito nesse tipo específico de colisão.
Bom, as duas bolas tem a mesma massa e apenas uma delas se movia antes da colisão bidimensional, por isso a equação das energias cinéticas ficou com essa cara:
Hhaan? Que cara?
Cara de Pitágoras...
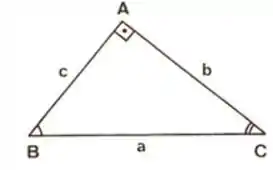
WTF?!?
Podemos pensar nessa equação de velocidades como os lados de um triângulo retângulo. Sendo o a hipotenusa e os catetos e .
Então, os vetores velocidade após a colisão teriam um ângulo de entre eles:
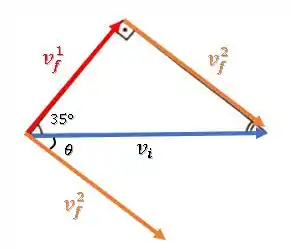
Ou sejaaaaaa...
Sempre que tivermos uma colisão exatamente como essa (mesma massa e corpo 2 parado), os dois corpos saem da colisão fazendo um ângulo de entre si.
Ahhh, a gente podia ter feito isso direto, então?
Até poderia hahah, mas é bom fazer esse passo a passo para evitar confusão.
Então, ficamos com a alternativa (C).
Resposta
Letra (C)