Calcule , onde está orientada pela normal exterior nos seguintes casos:
é a esfera ;
Passo 1
Eaew, belezinha?
Precisamos calcular a integral de superfície
Essa notação com produto exterior pode ser um pouco assustadora, então vamos considerar o seguinte formato equivalente
a esfera considerada é da forma
Para resolver isso, vamos usar o teorema da divergência de Gauss, já que o campo vetorial é meio chatinho! Temos que o teorema diz
Muitas vezes é mais simples resolver a integral tripla do que calcular explicitamente a integral de superfície! Vamos lá!
Passo 2
Vamos calcular de cara a divergência do campo vetorial, temos por definição que
em que
calculando as derivadas parciais e somando todos os termos, obtemos que a divergência tem a seguinte forma
bem mais simples não é? A nossa integral se torna então
Mas, e qual é a nossa região? Vamos trabalhar com ela um pouco!
Passo 3
O sólido pode ser representado pela seguinte figura
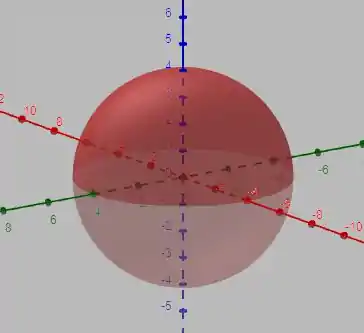
que é uma esfera arbitrária! Desta forma, o mais conveniente é escrever tudo em coordenadas esféricas dadas por
, e
lembrando que em coordenadas esféricas temos . Note que , que , e também que . Nossa integral se torna então
Vamos começar a nossa integração! Saca só!
Passo 4
Podemos começar com qualquer uma das variáveis uma vez que os limites de integração são todos constantes! Usualmente vale a pena começar com as variáveis trigonométricas porque muitas delas se anulam devido a simetrias das funções seno e cosseno! Portanto, integrando primeiramente em , temos que
Para resolver essas integrais vamos usar a substituição simples
e
mas antes disso, vamos usar que na primeira integral para obter
usando a substituição, notando que os limites se tornam e , temos que
Resolvendo todas as integrais conhecidas, temos que
Avaliando os limites de integração, temos que
Vamos continuar com as integrações agora!!
Passo 5
Integrando a variável , temos que
analogamente ao que fizemos na integração em podemos usar a relação de meio ângulo para o seno e obter
avaliando os limites de integração isso se torna
Agora só precisamos usar a regra do polinômio para integrar em , e assim obter
A questão foi isso! Te vejo na próxima! Tchau Tchau!