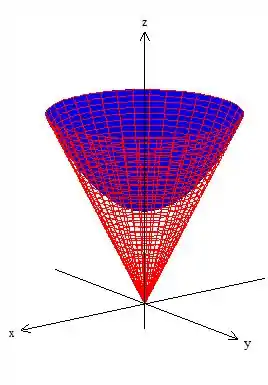
Questão 3: Seja a fronteira da região :
- Esboce a região .
- Calcular o fluxo do campo vetorial ao longo da superfície .
Passo 1
Para esboçar a região , basta ficar ficarmos atento para a sua definição:
Onde podemos tirar que ele é o cara que está dentro de duas superfícies conhecidas:
A primeira é um cone com vértice na origem:
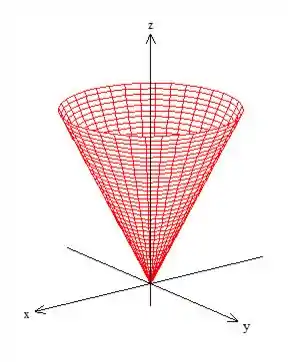
A segunda é um paraboloide com a concavidade pra cima e passando por :
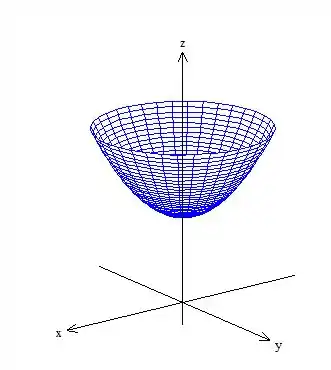
Veja você mesmo que a região é esse cara aqui:
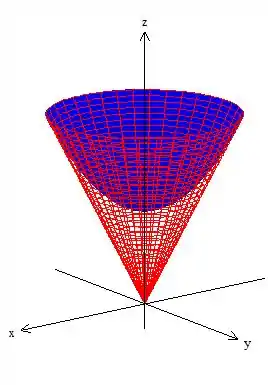
Passo 2
Bem, fluxo de um campo vetorial, nada mais é do que uma integral de superfície:
Porém repare você que como a superfície é fechada e definida por superfícies que não tem equações muito interessantes, calcular essa integral de superfície de forma direta pode nos dar certo trabalho. Além disso, se calcularmos o divergente de ...
Onde e são componentes do campo...
A gente percebe, então, que o divergente é muito interessante, nos indicando que vamos resolver o nosso problema pelo TEOREMA DE GAUSS!
Passo 3
Esse teorema nos iguala:
Mas, antes de aplicarmos essa igualdade, precisamos verificar as condições do Teorema que sempre nos exige:
- Uma superfície fechada delimitando .
- Uma orientação positiva.
- Um campo sem singularidades.
Nos três passos que seguem, vamos verificar cada condição. Bora?
Passo 4
A primeira condição:
“Uma superfície fechada delimitando .”
SIM! Isso já está sendo satisfeito:
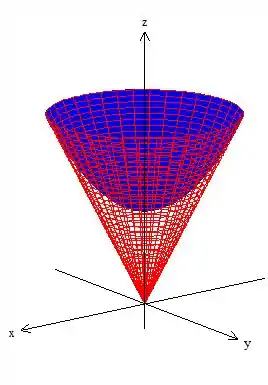
Passo 5
A segunda condição:
“Uma orientação positiva.”
Bem, isso significa que precisamos que a superfície fechada tenha vetores normais saindo apontando para fora. Como o exercício não nos deu uma orientação definida, podemos assumir essa condição sendo satisfeita, ok?
Passo 6
A terceira condição:
“Um campo sem singularidades.”
Se a gente der uma olhadinha no campo:
Percebemos que esse cara não tem problema algum de definição. Ou seja, ele não tem singularidades!
Passo 7
Com essas três condições analisadas, podemos prosseguir com o teorema !
Agora, troquemos o problema de resolver uma integral de superfície por um problema de cálculo de integral tripla.
Passo 8
Para resolver essa integral tripla então, devemos descrever o sólido de alguma forma:
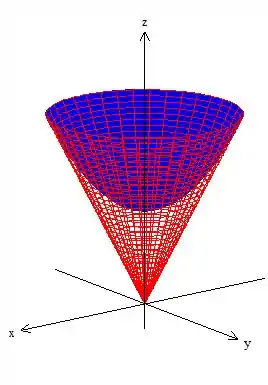
Como esse sólido varia entre cone e um paraboloide, podemos descrevê-lo em coordenadas cilíndricas, onde vamos trocar:
Com essa mudança temos:
Devemos prosseguir a descrição do sólido, então, encontrando a variação dos parâmetros , e .
Passo 9
Os parâmetros e , podem ser encontrados na projeção do sólido no plano !
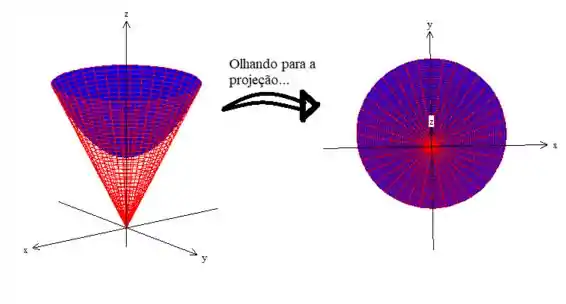
Veja que essa projeção nos indica que esses parâmetros variam na intersecção das duas superfícies delimitadora. A intersecção de uma forma matemática é a resolução do sistema com as duas equações das superfícies delimitadoras:
Resolvendo por Báskara...
Então...
E esse cara é um círculo de raio (como já dava para perceber na projeção)...
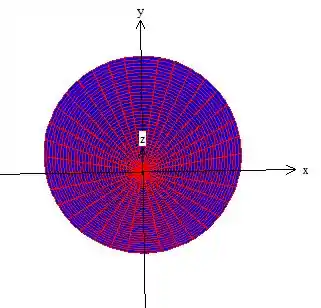
Logo...
Passo 10
Para a variação de , perceba que ele entra na região pelo cone e sai pelo paraboloide...
Em coordenadas cilíndricas...
Passo 11
Voltando para a integral tripla...
Calculando agora...
Pelo teorema de Gauss:
Resposta