Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Gauss

Ver Teoria
Exercício 63123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616264656667686970717273747576777879808182

Enunciado

Teorema de Gauss

Sejam S 1 = ( x , y , z ) | z 2 = x 2 + y 2 , 0 ≤ z ≤ 2 2 e S 2 = x , y , z | z 2 = 1 - x 2 - y 2 , 2 2 ≤ z ≤ 1 ; calcule

∬ S 1   F → . n → d S + ∬ S 2   F → . n → d S

Onde F → x , y , z = x y 2 + e z , y z 2 + e x , z x 2 + e y , a superfície S 1 está orientada pelo vetor normal com coordenada z negativa e S 2 pelo vetor normal com coordenada z positiva.

Passo 1

Vamos começar com um esboço disso aí, temos um pedaço de cone cortado e uma pedaço de esfera:

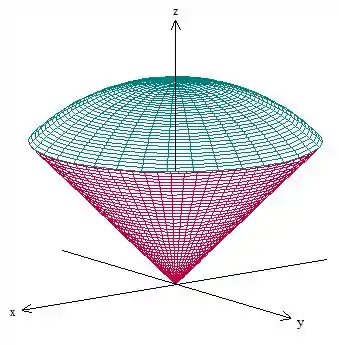
Passo 2

Como esse campo tem uma expressão bizara, vamos tentar usar o Teorema de Gauss. Começarmos calculando esse divergente:

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

d i v F → = y 2 + z 2 + x 2

Passo 3

Aplicando o teorema

∬ S 1   F → . n → d S + ∬ S 2   F → . n → d S = ∭ w   d i v F →   d V = ∭ w   y 2 + z 2 + x 2   d V

Sendo W a região na figura acima, orientada positivamente.

Passo 4

Agora precisamos escrever essa região matematicamente. Vamos usar coordenadas esféricas:

x = ρ sen ⁡ φ cos ⁡ θ

y = ρ sen ⁡ φ sen ⁡ θ

z = ρ cos ⁡ φ

J = ρ 2 sen ⁡ φ

Como vemos pela figura, o raio ρ vai desde zero até a superfície da esfera, dada por ρ = 1 . Sabemos que 0 ≤ θ ≤ 2 π porque temos uma volta completa em torno do eixo z .

O ângulo φ vai desde 0 até a superfície do cone, que, em coordenadas esféricas, é dada por:

ρ 2 cos 2 ⁡ φ = ρ sen ⁡ φ cos ⁡ θ 2 + ρ sen ⁡ φ sen ⁡ θ 2

ρ 2 cos 2 ⁡ φ = ρ 2 sen 2 ⁡ φ

t g   φ = 1

φ = π 4

Levando o que temos para a integral:

∭ w   y 2 + z 2 + x 2   d V = ∫ 0 π / 4 ∫ 0 2 π ∫ 0 1 ρ 2 ρ 2 sen ⁡ φ d ρ d θ d φ

= ∫ 0 π / 4 ∫ 0 2 π ∫ 0 1 ρ 4 sen ⁡ φ d ρ d θ d φ =

Passo 5

Agora é só resolver isso ai

= ∫ 0 π / 4 ∫ 0 2 π ρ 5 5 sen ⁡ φ 0 1 d θ d φ =

= 1 5 ∫ 0 π / 4 ∫ 0 2 π sen ⁡ φ d θ d φ =

= 1 5 ∫ 0 π / 4 θ   sen ⁡ φ 0 2 π d φ =

= 2 π   5 ∫ 0 π / 4 sen ⁡ φ d φ =

= - 2 π   5 cos ⁡ φ 0 π / 4 =

= 2 π   5 1 - 2 2 =

Isso nos dá

∬ S 1   F → . n → d S + ∬ S 2   F → . n → d S = 2 π   5 1 - 2 2

Resposta

2 π   5 1 - 2 2 =

Exercícios de Livros Relacionados

Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,