Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Gauss

Ver Teoria
Exercício 16123456789101112131415171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182

Enunciado

Seja F → x , y , z = cos ⁡ z 2 + x y 2 ,     x e - z ,   s e n y 2 + x 2 z .  

  1. Determine o rotacional de F → .

  2. Use o Teorema do divergente para calcular

∬ S F   d S

Onde S é a superfície do sólido limitado pelos paraboloides z = x 2 + y 2   e   z = 4 - x 2 - y 2 , orientada positivamente .

Passo 1

  1. Pra determinar o rotacional a gente gravou que:

r o t F = ( 2 y cos ⁡ y 2 - 0 ,   - 2 z   s e n z 2 - 2 x z ,   e - z - 2 x y )

( 2 y cos ⁡ y 2 ,   - 2 z   s e n z 2 - 2 x z ,   e - z - 2 x y )

Passo 2

  1. O Teorema do divergente (Gauss) nos diz que:

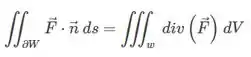
Onde o divisor é:

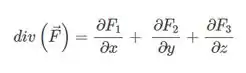
Então ficamos com:

F → x , y , z = cos ⁡ z 2 + x y 2 ,   x e - z ,   s e n y 2 + x 2 z .  

d i v F = y 2 + 0 + x 2 = x 2 + y 2

Passo 3

Agora vamos ver a região que estamos trabalhando.

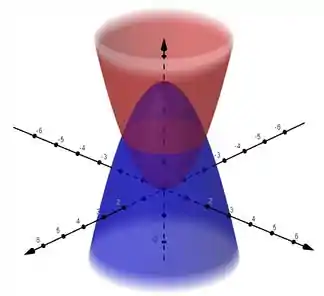
Se você observar, a interseção entre ambos os paraboloides forma uma circunferência. Isso já nos deixa uma dica de que usaremos outro tipo de coordenadas.

Passo 4

Usando coordenadas cilindicas, ficamos com:

x = r   c o s θ

y = r   s e n θ

z = z

J = r

Substitundo:

z = x 2 + y 2 → z = r 2

  z = 4 - x 2 - y 2 → z = 4 - r 2

Igualando as funções z = x 2 + y 2   e   z = 4 - x 2 - y 2 ,

x 2 + y 2 = 4 - x 2 - y 2

r 2 = 4 - r 2

r = 2

Ficamos então que θ da uma volta completa (0 a 2 π ), r vai de 0 a 2 e z varia entre as funções r 2 e   4 - r 2 .

Passo 5

Montando então a integral, sem esquecer o Jacobiano:

∬ S F   d S =   ∭ E x 2 + y 2 d V =   ∫ 0 2 π ∫ o 2 ∫ r 2 4 - r 2 r 2 r   d z   d r   d θ  

∫ 0 2 π ∫ 0 2 4 - 2 r 2 r 3   d r   d θ

2 π ∫ 0 2 π 4 r 3 - 2 r 5   d r  

2 π 2 4 - 2 3 6 = 8 π 3

Resposta

a   2 y cos ⁡ y 2 ,   - 2 z   s e n z 2 - 2 x z ,   e - z - 2 x y

b 8 π 3  

Exercícios de Livros Relacionados

Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,