Use o teorema do divergente para calcular o fluxo de
Através da superfície do sólido no primeiro octante limitado pelo cilindro e pelos planos , , e .
Passo 1
Vamos começar fazendo um gráfico dessa região, para entender melhor o problema. Temos um cilindro de raio centrado na origem, cortado pelos planos , , e , o que nos dá isso aqui:
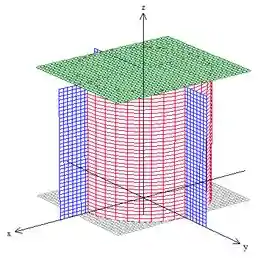
Fazendo esses cortes, a região que sobra é a seguinte:
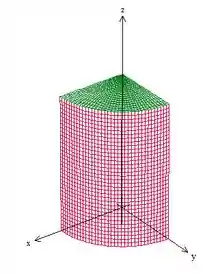
Como a região limitada por é fechada, sendo orientada positivamente, podemos aplicar o Teorema de Gauss:
Passo 2
Agora precisamos calcular . Temos:
Passo 3
Agora vamos montar a integral
Onde é o volume que vimos no passo 1.
Passo 4
Vamos agora, descrever essa região . Como nós temos um cilindro, parece uma boa usar coordenadas cilíndricas, certo? Temos:
Pela figura, vemos que , como já diz o próprio enunciado também. Vemos, ainda, que , o que representa de volta trigonométrica. Comos os valores de variam desde o eixo , onde até o cilindro, temos .
Isso nos dá
Passo 5
Agora vamos resolver a integral.
Integrando em relação a :
Agora em relação a :
Finalmente, em relação a :