Use o Teorema de Gauss para calcular o fluxo do campo
através orientada pelo vector normal tal que
Passo 1
Pelo teorema de Gauss, nosso primeiro parra pode ser calcular o divergente pra ver com o que estamos lidando aqui.
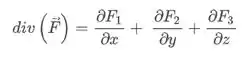
Opa, um divergente igual a zero é uma belezinha pra gente.
Com isso a gente conclui que a parte da integral tripla do nosso teorema vai ser zero.
![]()
No entanto, se você for observar a superfície qu estamos trablahando, ela não é fechada, que é uma das condições que o teorema exige.
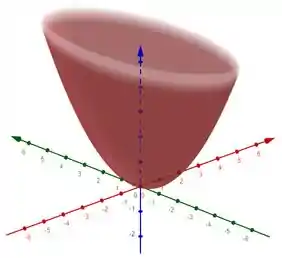
Então, pela regra do teorema, vamos precisar fechar nossa superfície.
Passo 2
Quando fechamos nossa superfície, o teorema fica:
Olhando pela definição de , é legal a gente pensar em fechar a superfície com o que limita ela.
.
Vamos então trabalhar com . Começamos parametrizando, onda fazemos uma parametrização explícita mesmo.
Vamos precisar ver onde estão variando os parametros, pra isso limitamos essa nova superfície com a anterior. Assim, com a interseção:
1)
2)
Passo 3
Calculando então nosso vetor normal ficamos com:
Montando então a integral de linha ficamos com:
Passo 4
Para podermos determinar essa área vamos usar umas coordenadas polares rápidas onde:
Com isso vemos a variação de
Remontando a integral ficamos com:
Resolvendo essa integral encontramos então: