Seja C a curva interseção do hemisfério da esfera de raio centrada na origem com o cilindro circular de raio e eixo , .
(a) Parametrize C.
(b) Para o campo vetorial
Calcule a circulação (trabalho) de ao longo de orientada no sentido anti-horário quando vista de cima.
Passo 1
a) Vamos começar colocando os pingos nos
Bem! Tá aqui as equações do hemisfério...
E tá aqui, a equação do cilindro...
Parametrizando o cilindro, temos que...
Logo;
Ficamos com;
Passo 2
Pelo próprio problema, temos que transformar a integral de superfície em uma integral de linha. Ora! O teorema de Stokes já nos dá essa igualdade:
Agora, para aplicar essa igualdade existem algumas restrições que precisamos ter cuidado:
1º - Uma curva fechada delimitando uma superfície .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Bem, a superfície que ele nos deu é uma esfera de raio ( )
Mas a última restrição é que queremos só a parte de cima, afinal, temos um . Então eis a superfície (O hemisfério norte):
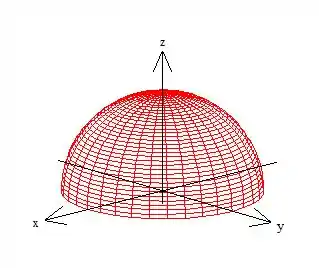
Passo 3
Muito bem, veja que essa superfície tem uma borda que chamaremos de curva , e essa curva é uma circunferência que está destacada em vermelho escuro:
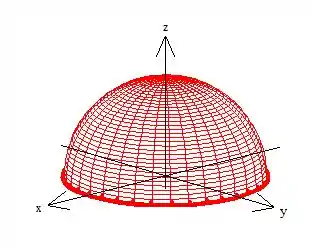
Para sabermos a equação dessa circunferência, basta pegar as duas equações e resolver o sistema...
Logo, se trata de uma circunferência de raio , pois , e que está em cima do plano (ou o plano , como preferir ).
Passo 4
As outras duas condições do problema nos pedem que tenhamos:
2º - Sem singularidades na função Vetorial.
Ora, sim! Basta ver o campo
Para você perceber que o campo não tem nenhum bug ou singularidade, como uma divisão por em algum ponto ou algo assim.
3º - Superfície orientada positivamente.
Aqui o que temos que fazer é garantir que o conjunto curva-superfície estejam orientadas positivamente. Pow, como o vetor aponta pra cima (o próprio problema nos disse isso quando disse orientação ascendente):
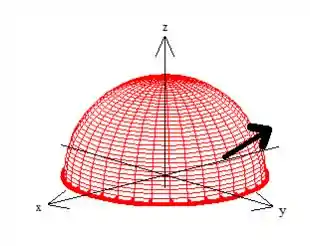
Pela regra da mão direita temos que ter uma curva girando no sentido anti-horário quando vista de cima:
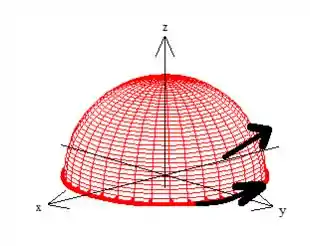
Agora elas estão sim orientadas positivamente, saca?
Passo 5
Com a as três condições de boa, podemos aplicar a igualdade sem problema algum:
Para resolver a integral de linha pelo método direto que conhecemos, façamos:
1º - Parametrizar a curva .
2º - Encontrar .
3º - Encontrar em termos da parametrização.
Passo 6
Como vimos, a curva é uma circunferência de raio que está em cima do plano ... Essa circunferência como vimos tem equação...
Então por semelhança com equação fundamental ...
O da curva é bem conhecido...
Logo a parametrização escrita de uma forma mais elegante é...
Onde dá uma volta completa girando de até , formando à curva redonda completa, saca?
Passo 7
A nossa segunda tarefa é determinar o termo ...
Aqui só tem um detalhe muito importante. Para onde a curva gira com essa parametrização? Ora, essa e uma parametrização clássica onde a curva gira sempre no sentido anti-horário quando vista de cima:
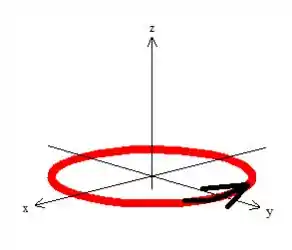
Ai então eu te pergunto, é isso que a gente quer? Sim! Isso já acontece, então nem vamos ter que alterar nada...
Sacou? Fique atento a isso! 😉
Passo 8
Como terceira e última tarefa antes de integrar tudo, só temos que transformar o campo ...
Como ...
Passo 9
Jogando tudo na integral de linha...
Calculando o produto escalar...
Integrando essa parada lembrando que
Resposta
a)
b)