Sejam um campo vetorial de classe e . Considere as seguintes afirmações, nas quais denota a esfera de centro e raio orientada pela normal exterior , e a bola fechada de centro e raio .

(I) Se , existe tal que .

(II) Se , existe tal que .

(III) Se , para todo , tem-se .

São verdadeiras, apenas: (Escolha uma)

a) Nenhuma

b) Todas

c) II e III

d) I

e) II

(I) Ele diz que se , ou seja, se no ponto , o divergente vale zero, para algum valor de positivo, podemos ter que

Cara, ele está relacionando a integral de superfície, de uma superfície fechada, com vetor normal exterior em um campo de classe , ao divergente. Quem a gente pode usar para resolver essa? O teorema de Gauss!

Gauss diz que:

Sendo a região dentro de uma superfície fechada , ou seja, é a nossa esfera e , a região dentro dela.

Para esse lado direito zerar, temos que o lado esquerdo deve zerar, e isso só acontece se a integral tripla zerar.

Mas repara, que para essa integral zerar, temos duas situações possíveis:

- ou , para todos os pontos.

- ou a soma de de todos os pontos dentro de dá zero.

Maaas, a afirmativa só diz que o divergente é zero no ponto , não temos informações sobre os outros pontos dentro da esfera, então não podemos dizer que estamos em algumas dessas duas situações acima.

Logo, a gente não pode afirmar com certeza que a integral vai zerar para algum valor de . Essa vai ser falsa.

(II) Ele diz que se no ponto , o divergente de for positivo, então existe algum valor de que faça a integral de superfície

Também ser positiva. Vamos usar Gauss de novo aqui. Repara:

Para esse lado direito ser positivo, temos que o lado esquerdo deve ser também. Mas repara, que para essa integral ser positiva, temos duas situações possíveis:

- ou , para todos os pontos, e aí, para qualquer valor de , ou seja, para qualquer tamanho de esfera, a soma do divergente em todos os pontos dentro da esfera vai ser positiva.

- ou a soma de de todos os pontos dentro de uma esfera de um raio adequado, dá um número positivo.

Como a gente só tem a informação de um ponto, não podemos afirmar que a primeira é verdade. Mas e a segunda?

Cara, vamos lembrar da definição de divergente:

Ele vai ser uma função escalar. E como nosso campo é de classe (tem todas as derivadas de primeira ordem contínuas), a soma dessas derivadas também vai ser uma função contínua.

Isso nos diz que vai ser uma função contínua com domínio em , no espaço 3D.

Agora pensa comigo, se num ponto, essa função contínua é positiva, nos pontos próximos, ela também vai ser positiva. Isso acontece com uma função com domínio só em , por exemplo:

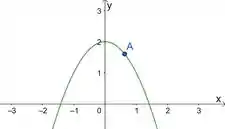
Repara, que a soma de pontos que essa função assume quando estamos próximos de , vai ser um número positivo.

Mas se a gente pegar um intervalo muito grande, com números mais distantes de , vamos ter pontos onde a função assume valores negativos também, fazendo com que a soma possa dar um número negativo.

Acontece algo análogo para funções com domínio em , para pontos próximos de um ponto onde ela assume um valor positivo, ela vai também assumir valores positivos.

Então, se a gente posicionar uma esfera, com um raio pequeno o suficiente para englobar a região onde ela assume só valores positivos (ou majoritariamente, valores positivos), a integral tripla vai ser positiva.

O que faz com que, para valores adequados de , tenhamos

Então essa é verdadeira.

(III) Cara, aqui ele tá dizendo que se o divergente no centro da esfera for positivo, então, para qualquer , teremos a integral de superfície positiva.

Estamos com a situação parecida com a anterior:

Mas aqui, para o lado direito ser sempre positivo para qualquer valor de (para esferas de qualquer tamanho), temos que todos os valores que assume precisam ser positivos.

Só que não temos certeza se isso acontece. A gente só sabe que ele é positivo em um ponto. Logo, essa vai ser falsa.