Considere a solução do problema de valor inicial (PVI) , , . Encontre o limite de quando em cada um dos casos abaixo:
(a)
(b)
(c)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão temos uma EDO de segunda ordem homogênea de coeficientes constantes dada por .
Foi dito que a solução quando é e quando a derivada da solução em , .
O objetivo principal dessa questão é obter a solução e calcular o limite de para quando tende ao infinito em três ocasiões: quando , quando e quando .
Como podemos fazer isso?? 🤔🤔
Primeiro de tudo, vamos obter a solução dessa EDO. Lembrando que para uma EDO de segunda ordem homogênea com coeficientes constantes, a solução é dada caso o .
Substituindo por , por e por na EDO, vamos obter a equação que a solução nos dá e .
Bora começar? 😎
Passo 2
Primeiro vamos encontrar o . Fazendo as substituições que indicamos no passo anterior, vamos ter
Por Bhaskara, a solução dessa equação é dada por
Com isso, tiramos que
Logo a solução da EDO será
Como temos um problema de valor inicial onde , vamos obter os valores de e .
Temos uma primeira relação entre e . Agora temos que derivar para obter a segunda relação.
Tranquilo até aqui? 👀
Passo 3
Derivando pela regra da cadeia (a derivada de dentro multiplicado pela a derivada de fora), ou seja
Substituindo por , temos
Com isso, temos um sistema de duas equações
Isolando na primeira equação e substituindo na segunda, temos
Substituindo em
Com e obtidos, a solução completa é dada por
Interessante, não é?
Passo 4
Agora temos que calcular o limite dessa função quando tende ao infinito
Ou seja
Como o limite da soma é igual a soma dos limites, temos
Podemos tirar as constantes para fora dos limites, resultando em
Pelos gráficos de (em verde) e (em azul), temos
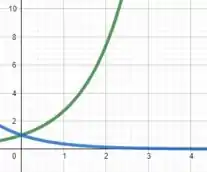
Observamos que no infinito, tende a e tende a , ou seja
Se e resulta em uma constante qualquer, então
Dessa forma o numerador vai resultar em um valor positivo, já que ou seja . Logo
Se , temos
Já vimos que tende a quanto tende ao infinito, então
Está acompanhando?
Passo 5
Por fim, se , temos
Da primeira constante, podemos dizer que
Com isso, podemos afirmar que a primeira constante é negativa
Já para a segunda constante
Essa constante resulta em um número que não vai fazer diferença, já que vai para no infinito.
E como a primeira constante resulta em um valor negativo, então
E essas são as possibilidades dos casos a), b) e c)!
É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta
a)
b)
c)