Esboce o gráfico
Passo 1
Para esboçar o gráfico da função
siga os seguintes passos:
O domínio da função é o conjunto de todos os valores de para os quais a função está definida.
Neste caso, a função é definida para todos os números reais, já que a exponencial é definida para todos os valores de
Portanto, o domínio da função é (todos os números reais).
Para encontrar onde a função cruza o eixo , defina
No entanto, esta função nunca é igual a zero para qualquer valor real de porque o numerador é sempre positivo e o denominador é sempre positivo.
Portanto, a função
não cruza o eixo x, o que significa que não há pontos de interseção com o eixo x.
Passo 2
Comportamento da Função para Tendendo ao Infinito
À medida que tende ao infinito positivo, o termo dominante é e a função se aproxima de 1 à medida que aumenta.
Isso ocorre porque a exponencial se torna muito maior do que 1, e a fração se aproxima de 1.
À medida que tende ao infinito negativo, o termo no numerador torna-se muito pequeno em comparação com 1 no denominador, e a função se aproxima de 0
Encontrando o Comportamento para
Substituindo na função:
Portanto, o ponto em que a função cruza o eixo y é
Com base nas informações acima, você pode esboçar o gráfico da função da seguinte maneira:
- O domínio da função é (todos os números reais).
- A função não cruza o eixo x, pois não há soluções para .
- À medida que tende ao infinito positivo, a função se aproxima de 1.
- À medida que tende ao infinito negativo, a função se aproxima de 0.
- A função cruza o eixo y em
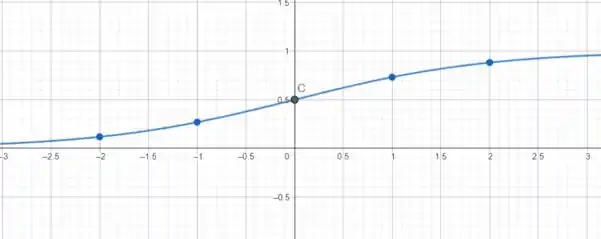
O gráfico será uma curva suave que se aproxima de à medida que aumenta e de à medida que diminui, com um ponto de interseção em .
A função nunca atinge os valores 0 ou 1 e está sempre contida no intervalo .
Passo 3
Gráfico
Resposta
Vide o passo a passo.