Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Esboço de Gráfico

Ver Teoria
Exercício 841234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283858687888990919293949596979899100

Enunciado

Para a função

f x = x 2 - x ³ 3

Determine os pontos críticos, pontos de inflexão, intervalos de crescimento e decrescimento e o estudo da concavidade.

Passo 1

Vamos começar achando os pontos críticos.

f ' x = 0

2 x - 3 x ² 3 x 2 - x 3 2 3 = 0

2 x - 3 x 2 = 0

x = 0 ;   x = 2 3

Uma observação importante é que a derivada de f não está definida para x = 0 e x = 1 , pois esses pontos tornam o denominador nulo. Portanto, apenas x = 2 3 é ponto critico.

Passo 2

Para saber os intervalos de crescimento e decrescimento temos que analisar o sinal da derivada de f .

f ' x = 2 x - 3 x ² 3 x 2 - x 3 2 3

Seu gráfico é:

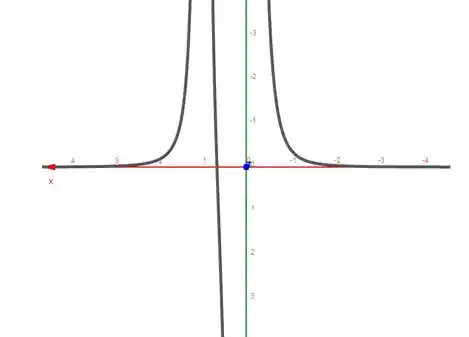
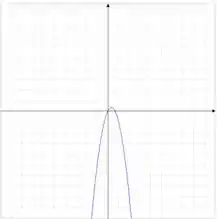
f ' ( x ) depende apenas de 2 x - 3 x ² , pois 3 x 2 - x 3 2 3 é sempre positivo. Como 2 x - 3 x ² , é uma parábola de concavidade pra baixo que corta eixo x em x = 0   e   x = 2 3 , ocorre o seguinte:

A derivada é positiva entre 0 e 2 3 e negativa para x < 0 e x > 2 3 .

Assim:

Intervalo de decrescimento de f : x < 0   e   x > 2 3

Intervalo de crescimento de f : 0 < x < 2 3

Passo 3

Temos que saber onde a função é côncava pra cima ou côncava pra baixo. Como que isso é feito? Analisando o sinal da segunda derivada. Então vamos com calma, primeiro temos que

derivar f ' ( x ) :

f ' ' x = 3 2 - 6 x x 2 - x 3 2 3 - 2 2 x - 3 x 2 2 x 2 - x 3 - 1 3 9 x 2 - x 3 4 3       →

f ' ' x = 3 2 - 6 x x 2 - x 3 2 3 - 2 2 x - 3 x 2 2 x 2 - x 3 1 3 9 x 2 - x 3 4 3

Colocando todo mundo pelo mesmo denomidador para dar uma organizada nesse monstrinho...

f ' ' x = 3 2 - 6 x x 2 - x 3 2 3 x 2 - x 3 1 3 x 2 - x 3 1 3 - 2 2 x - 3 x 2 2 x 2 - x 3 1 3 9 x 2 - x 3 4 3         →

f ' ' x = 3 2 - 6 x x 2 - x 3 - 2 2 x - 3 x 2 2 9 x 2 - x 3 5 3         →

f ' ' x = 3 2 x 2 - 2 x 3 - 6 x 3 + 6 x 4 - 2 4 x 2 - 12 x 3 + 9 x 4 9 x 2 - x 3 5 3       →

Finalmente...

f ' ' x = - 2 x 2 9 x 2 - x 3 5 3

Passo 4

Vamos estudar o sinal da segunda derivada então? Para isso, note que o sinal do denominador da segunda derivada, embora tem aquele 5 3 , isso não influencia no sinal, pois 5 e 3 são impares! Veja só, vamos estudar o denominador primeiro:

  • O sinal só de x 2 - x 3 fazendo a separação...

    • x 2 - x 3 = x ² ( 1 - x )

    É...

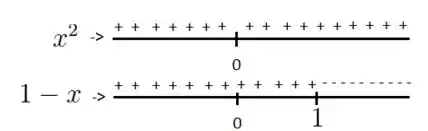
    Então multiplicando os sinais...

    Veja que esse sinal é o mesmo do denominador conforme comentamos acima:

  • Pelo fato do sinal do denominador ser esse cara aqui...

Concluímos que o sinal da derivada então é a divisão desses dois últimos:

Nos intervalos em que a segunda derivada é positiva, a função é côncava pra cima. Já nos intervalos em que a segunda derivada é negativa, a função é côncava pra baixo.

Portanto

• A função f tem concavidade para cima para x >   1   e   x ≠ 0

• A função f tem concavidade para baixo para x < 1

Passo 5

Os pontos de inflexão são aqueles em que a função muda de concavidade, certo? Como vimos no passo anterior, para a função f isso ocorre quando

x = 1

Então, o ponto de inflexão é em:

x = 1

Resposta

x = 2 3 é ponto critico

Intervalo de decrescimento de f : x < 0   e   x > 2 3

Intervalo de crescimento de f : 0 < x < 2 3

A função f tem concavidade para cima para x >   1   e   x ≠ 0

A função f tem concavidade para baixo para x < 1

Ponto de inflexão x = 1

Exercícios de Livros Relacionados

Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2