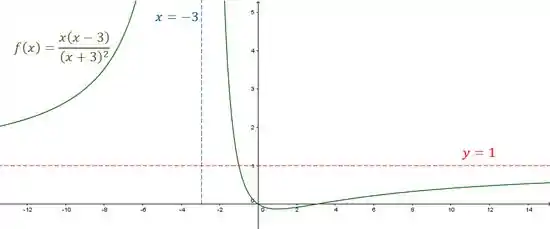
Seja
- Encontre as assíntotas horizontais e verticais, caso existam, da função .
- Determine os intervalos onde a função é crescente ou decrescente. Encontre também os pontos de máximo e mínimo locais e absolutos da função, assim como os respectivos valores da função nesses pontos.
- Determine os intervalos onde a função é côncava para cima ou para baixo, assim como os seus pontos de inflexão.
- Use as informações dos itens (a)-(c) para esboçar o gráfico de .
Passo 1
(a)
Vamos começar pelas assíntotas verticais. Elas aparecem em pontos onde a função não está definida.
A só não está definida quando seu denominador se anular, isto é
E temos que
Então de fato é uma assíntota vertical da .
Passo 2
Agora vamos pras assíntotas horizontais. Basta calcular os limites da função no infinito:
Usando l’Hôpital:
? L’Hôpital de novo!
Pro limite em vai ser praticamente a mesma coisa, basta aplicar l’Hôpital várias vezes seguidas:
Então é a única assíntota horizontal da .
Passo 3
(b)
Nesse item precisamos da derivada da . Sendo que
Derivando com a regra do quociente :
Dividindo por em cima e embaixo:
Desenvolvendo isso aí:
Passo 4
Pra descobrir como cresce a , temos que estudar o sinal dessa derivada. Então vamos montar um quadro de sinais bonitinho.
Só uma observação antes:
Ou seja:
Enfim, vamos ao quadro:
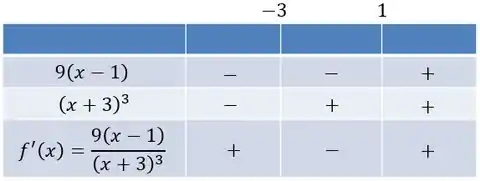
Daí, pelo teste da primeira derivada, concluímos que é crescente no intervalo e decrescente no intervalo .
Passo 5
A questão também pediu os máximos e mínimos.
Vimos lá atrás que em a função explode pra , lembra? Isso significa que não tem ponto de máximo global.
E na verdade, isso significa também que não tem ponto de máximo local! Os pontos de máximo local aparecem quando o sinal da derivada muda de pra né? O único ponto onde isso acontece é , que é justamente o ponto onde a função explode pra infinito.
Já em o sinal da derivada muda de pra , e não temos nenhum problema de indeterminação em , então esse ponto é um ponto de mínimo local.
O valor desse mínimo é:
Olhando o quadro de sinais e levando em conta que
Podemos ver que também é ponto de mínimo global da função.
Passo 6
(c)
Agora precisamos da derivada segunda da . Lembrando que
Derivando de novo com a regra do quociente:
Dividindo o numerador e o denominador por :
Passo 7
Como , nem precisamos fazer quadro de sinal.
Basta ver o sinal de :
Portanto, tem concavidade para cima no intervalo e concavidade para baixo no intervalo .
O único ponto de inflexão da é onde a concavidade muda: . E temos que
Passo 8
(d)
Podemos resumir todas as informações que achamos numa tabelinha:
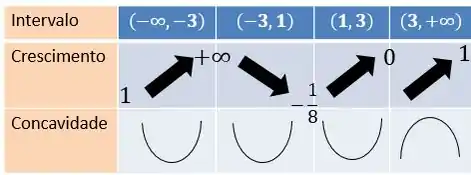
Agora é só esboçar a criança:
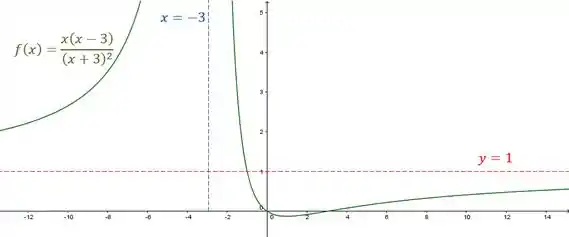
Resposta
(a)
Assíntota vertical
Assíntota horizontal:
(b)
Crescimento no intervalo
Decrescimento no intervalo
Ponto de mínimo local e absoluto:
Não tem ponto de máximo.
(c)
Concavidade para cima no intervalo
Concavidade para baixo no intervalo
(d)