Questão 3:
Seja a função dada por
- Determine o domínio da função .
- Determine o(s) intervalo(s) onde é decrescente.
- Determine as equações das retas assíntotas horizontais e verticais do gráfico de , caso existam.
- Utilizando as informações obtidas nos itens anteriores, esboce o gráfico de e suas retas assíntotas, caso existam.
Passo 1
Bem, vamos então analisar o domínio dessa parada:
Sempre começamos a análise de um domínio supondo que o domínio é o maior possível, ou seja, toda a reta real . E depois vamos eliminando pedaços onde a função não funciona. Veja só:
Para começar, sabemos em uma fração, nunca podemos ter o denominador igual a zero...
Então nesse caso não podemos ter . Repare que o domínio já se restringiu. Antes ele era todo o agora ele é tirando o .
Mas ainda não acabou. Sabemos que em um logaritmo, o logarítmando dever ser maior que
Bem, o denominador sempre é positivo por causa do quadrado. Mas não podemos falar o mesmo do nominador. Então temos que encontrar o domínio onde o denominador é maior que ...
Encontrando os zeros dessa equação...
Como esse cara é uma parábola com a concavidade pra cima...
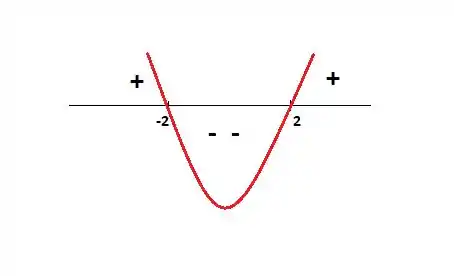
Perceba que ela assume valores positivos nos intervalos...
Com esse cara positivo, o logaritmando também é! Já sabíamos que não podia entrar na brincadeira, mas ele já está incluído sesse intervalo, saca? Então o Domínio da função é esse são esses intervalos aí:
Passo 2
Cara, como precisamos avaliar o decrescimento, o que devemos fazer é avaliar o sinal da primeira derivada, afinal de contas...
Então bora derivar !
Passo 3
Aplicando a regra da cadeia para derivar...
Agora aplicando a regra da fração...
Passo 4
Temos então que analisar o sinal dessa função. Perceba que se o denominador for positivo, o a função derivada é negativa e essa é a única forma disso acontecer...
Como para todo domínio de , , então a função derivada é sempre negativa no domínio de , o que implica que é sempre decrescente no seu domínio, saca?
Passo 5
Bem, para analisar se o gráfico têm assíntotas horizontais, calculemos os limites da função tendendo aos infinitos...
Como está indo ao infinito, acho muito válido multiplicar e dividir por ...
Quando vai para o infinito, essa fração de vai a ...
Quanto ao limite no infinito negativo...
Quando o vai pro negativo esses caras continua indo a zero igual a ...
Então a única assíntota horizontal que temos é...
Passo 6
Para averiguar se têm assíntotas verticais, calculemos o limite da função, mas agora indo para os dois pontos de problema da função (pontos de limites do domínio) no caso...
Calculando esse primeiro limite...
Quando esse cara tende a pela esquerda, ou seja, por valores menores que , como , esse termo é um pouco maior que , levando esse cara para o ...
Então é uma assíntota vertical.
Passo 7
Calculando o outro limite...
Como ...
Quando esse cara vai a pela direita , essa fração vai ao infinito positivo...
Logo, é uma outra assíntota vertical
Passo 8
Para desenhar o gráfico dessa função , vamos unir as informações que conseguimos até agora, ou seja:
O domínio da função é de .
A função é inteiramente decrescente nesse domínio.
Além disso, quando e .
Quando vai ao infinito positivo ela tende a reta assíntota , e quando vai ao infinito negativo ela também tende a essa reta...
Só podemos estar falando de...
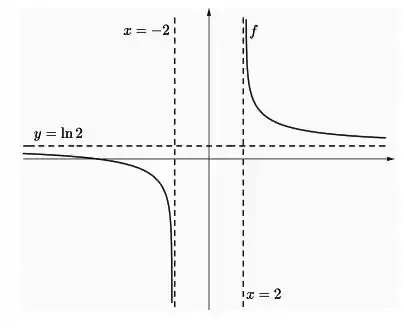
Onde as assíntotas são essas retas aí saca? :D
Resposta
Assíntotas horizontais: e .
Assíntotas verticais: