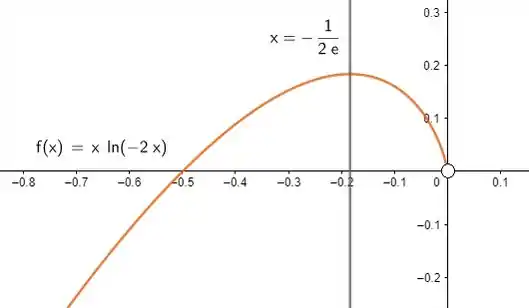
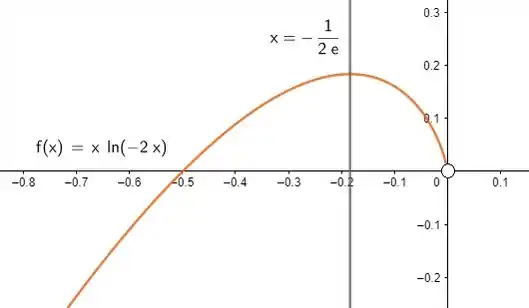
4) Seja a função dada por:
- Determine o domínio da função
- Determine as equações das retas assíntotas horizontais do gráfico de , caso existam.
- Determine as equações das retas assíntotas verticais do gráfico de , caso existam.
- Determine o(s) intervalo(s) de crescimento e de decrescimento de .
- Determine o(s) intervalo(s) onde o gráfico de f tem concavidade voltada para cima e onde tem concavidade voltada para baixo
- Esboce o gráfico de e suas retas assíntotas horizontais e verticais, caso existam
Passo 1
Questão completa essa em! Então vamos lá, começando pelo domínio. Como temos uma parcela logarítma nessa função, não vale qualquer não em! O interior de um logarítimo tem que sempre ser positivo. Sendo assim, temos:
Então o domínio da função vai ser
Passo 2
Agora bora ver as assíntotas horizontais. Pra vermos se tem assíntotas, temos que fazer os seguintes limites
Pro primeiro limite, vamos ter:
Agora, pro segundo limite, como o domínio é:
Calcular ele não faz sentido. Sendo assim, como não tivemos limite tendendo a um número, não vamos ter assíntota horizontal, beleza?
Passo 3
Pra ver as assíntotas horizontais, temos que ver o limite para os pontos que “dão problema” na nossa função. Veja bem, a função não está nem definida, e ela está, sem problema algum. O ponto que dá problema então é . Fazendo o limite, achamos então:
Opa, deu um número! Não é uma assíntota então! Seria assíntota vertical se tivéssemos achado . Seguindo então!
Passo 4
Pra ver intervalo de crescimento e decrescimento, temos que ver quando a inclinação da reta tangente é positiva ou negativa. E que melhor forma de fazer isso que usando a primeira derivada, que é exatamente essa inclinação? Usando a regra do produto então, derivamos:
Por fim, ficamos com:
Bem, como queremos saber quando essa primeira derivada muda de sinal, temos que ver primeiro quando ela não tem sinal, ou seja, precisamos achar suas raízes. Pra isso, igualamos à , beleza? Bora lá:
Então pra gente checar o sinal da derivada, vamos escolher intervalos que envolvam essa raíz que achamos e o domínio da função. Os intervalos vão ser:
Para o primeiro intervalo, vamos testar . Vamos ter:
Para o segundo intervalo, vamos testar . Vamos ter:
Como a primeira derivada positiva quer dizer função crescente, e a primeira derivada negativa função decrescente, vamos ter:
Passo 5
Agora, pra concavidade, a ideia é a mesma do intervalo de crescimento e decrescimento, ok? O que vai mudar agora é que vamos analisar a segunda derivada, pra isso:
Derivando então, vamos ter:
E veja só! Essa função nunca zera! Porém, se:
Como não está definido na nossa , então a segunda derivada vai ser sempre negativa em todo o domínio! E segunda derivada negativa quer dizer concavidade pra baixo!
Passo 6
Temos tudo viu? Só pra ficar bem claro, o que vimos foi:
Juntando todas essas informações, esboçamos: