Considere a função dada por:
- Determine, caso exista(m):
(a.1) O(s) intervalo(s) de crescimento e decrescimento de .
(a.2) O(s) ponto(s) de máximo local e de mínimo local de .
(a.3) O(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
(a.4) O(s) ponto(s) de inflexão do gráfico de .
b) Faça um esboço do gráfico de indicando explicitamente o(s) ponto(s) de máximo, de mínimo e de inflexão determinado(s) nos itens anteriores. Esboce também a(s) reta(s) tangente(s) ao gráfico de no(s) ponto(s) em que a derivada é zero e no(s) ponto(s) de inflexão.
Passo 1
(a.1) Para saber os intervalos de crescimento e decrescimento temos que analisar o sinal da derivada de . Então vamos começar derivando a função:
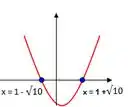
Assim:
Intervalo de crescimento de :
Intervalo de decrescimento de :
Passo 2
(a.2) Vamos achar os pontos críticos para podermos determinar os máximos e mínimos locais, se existirem.
A próxima etapa é fazer o Teste da Primeira ou da Segunda derivada. Nesse caso, já que temos o gráfico do item anterior pra ajudar, vamos fazer o Teste da Primeira Derivada, ou seja, analisar o sinal da derivada perto dos pontos críticos. Olha só:
- Em a derivada muda de positiva para negativa, logo esse é um ponto de máximo local
- Em o sinal da derivada não muda, logo não é nem máximo nem mínimo local
- Em a derivada muda de negativa para positiva, logo esse é um ponto de mínimo local
Passo 1
(a.3) Temos que saber onde a função é côncava pra cima ou côncava pra baixo. Como que isso é feito? Analisando o sinal da segunda derivada. Então vamos com calma, primeiro temos que derivar :
Agora partiu encontrar as raízes desse polinômio!
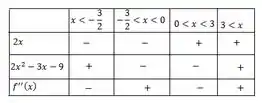E finalmente, vamos estudar os sinais:
Nos intervalos em que a segunda derivada é positiva, a função é côncava pra cima. Já nos intervalos em que a segunda derivada é negativa, a função é côncava pra baixo.
Então, nos intervalos e a função é côncava pra cima e nos intervalos e a função é côncava pra baixo.
Passo 2
(a.4) Os pontos de inflexão são aqueles em que a função muda de concavidade, certo? Como vimos no item anterior, para a função isso ocorre quando
Então, os pontos de inflexão são:
Passo 3
Como é uma função polinomial, seu domínio é o próprio conjunto dos números reais, sem nenhuma restrição. Já que não temos restrições no domínio, a função não tem assíntotas verticais. E fazendo os limites adequados para descobrir assíntotas horizontais, você vai ver que também não tem assíntotas horizontais. Então estamos prontos para esboçar o gráfico, que vai ficar desse jeito:
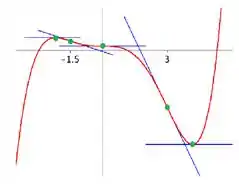
Resposta
(a.1) Intervalo de crescimento de :
Intervalo de decrescimento de :
(a.2) é um ponto de máximo local e a é um ponto de mínimo local
(a.3) Nos intervalos e a função é côncava pra cima e nos intervalos e a função é côncava pra baixo
(a.4)
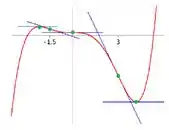b)