Seja .
Determine o domínio de e os intervalos de crescimento e decrescimento de .
Verifique que . Determine e estude a concavidade de .
Calcule os limites necessários e esboce o gráfico de .
Passo 1
Para pensarmos em crecimento e decrescimento de temos que observar o sinal da derivada primeira. Vamos calcular pela Regra do Quociente:
Como o termo exponencial é sempre positivo e o é uma potência par, sendo positivo também, vemos que o sinal só depende de . Vou buscar a região onde é maior que para, a partir disso, determinar onde é crescente, sendo o resto do domínio decrescente, à excessão do ponto que é onde e , que não está definido no domínio:
Fazendo o quadro de sinais:
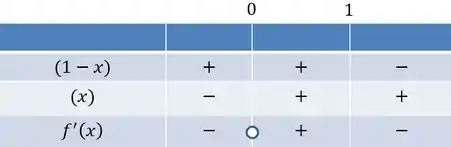
Vamos que será crescente em quando estiver no intervalo e decrescente quando pertencer a , sendo que em teremos um ponto crítico de máximo, já que a derivada é positiva antes de e negativa depois de , sendo nula no ponto.
Passo 2
Vamos calcular a derivada segunda de :
Vamos usar a Regra do Produto e do Quociente:
Ora, comparando com o formato da derivada apresentada no enunciado da letra nós notamos que a constante vai valer .
Passo 3
Analisando agora os intervalos de concavidade para cima e para baixo da função, devemos observar o sinal de . Sabemos, já que a exponencial será sempre positivo. A parábola de cima pode ter seu sinal analisado levando em conta que é côncava para cima e tem duas raízes que podemos descobrir por Bhaskara. Já o será positivo para e negativo para . Vamos descobrir as raízes da parábola do denominador e fazer o quadro dos sinais:
O quadro fica assim então:
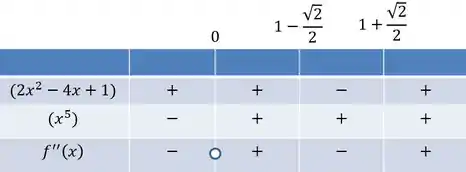
Logo, a concavidade é para cima quando está em e para baixo quando pertence a . Temos pontos de inflexão em e .
Passo 4
Vamos primeiro buscar as assíntotas horizontais usando o limite de em :
Achamos uma mesma assíntota horizontal, para , o que significa que não existem assíntotas oblíquas também. Para assíntotas verticais devemos usar o limite onde o domínio da função não está definido:
Para fugir da indeterminação vamos usar L’Hospital:
Concluímos, portanto, que em temos uma assíntota vertical, porém do lado de a função se aproxima de tendendo a . Para valores de ela se aproxima de .
Passo 5
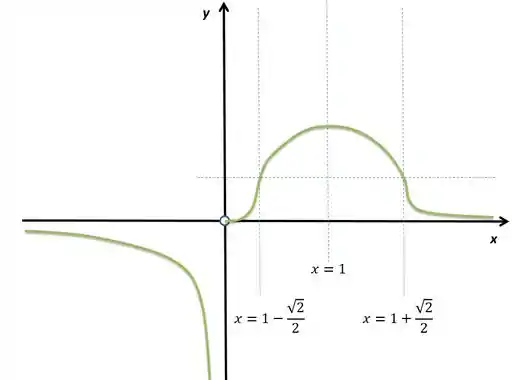
Agora podemos esboçar o gráfico, com as informações que possuímos:
- Domínio de corresponde a .
- será crescente em quando estiver no intervalo e decrescente quando pertencer a , sendo que em teremos um ponto crítico de máximo.
- A concavidade é para cima quando está em e para baixo quando pertence a . Temos pontos de inflexão em e .
- Assíntota horizontal: ; Assíntota vertical: .
O gráfico será algo parecido com isso: