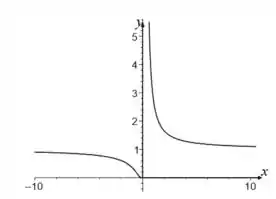
Esboce o gráfico de
Passo 1
Para começar, vamos determinar o domínio da função. A única restrição é no ponto , em que a função não está definida. Então o domínio é
Passo 2
Agora, vamos ver se a função tem alguma paridade, ou seja, se ela é uma função par ou uma função ímpar.
- ?
Não. Exemplo:
-?
Não. Exemplo:
Passo 3
Chegou a hora de determinar se a função tem assíntotas. Vamos começar pelas verticais. Essas ocorrem perto de pontos de descontinuidade da função. Nesse caso temos o ponto em que a função é descontínua. Vamos ver o comportamento dela perto desse ponto.
Então é uma assíntota vertical para a derivada de quando vai a zero pela direita.
Agora vamos ver as assíntotas horizontais.
Então é assíntota horizontal.
Passo 4
Esse passo vai ser dedicado ao estudo do crescimento da função. Temos que derivar e ver onde a derivada é positiva e negativa.
Como o sinal da derivada só será afetado por , mas veja só, para todo no domínio, logo sempre. Ou seja
Como a derivada é sempre negativa, significa que a função é estritamente decrescente.
Passo 5
Agora vamos determinar os máximos e mínimos da função, se existirem. Primeiro temos que achar os pontos críticos.
A equação acima não tem solução real, logo não há pontos críticos, portanto, não há máximo nem mínimo.
Passo 6
Estamos quase terminando. Falta estudar a concavidade da função. Para isso, temos que fazer a segunda derivada, lembra?
Note que e então só o influencia no sinal. Vamos ver como.
- Quando : e a função tem concavidade para baixo
- Quando : e a função tem concavidade para cima
O ponto é ponto de inflexão.
Passo 7
Pronto! Agora podemos juntar todos os dados que descobrimos e fazer o esboço do gráfico, que fica assim:
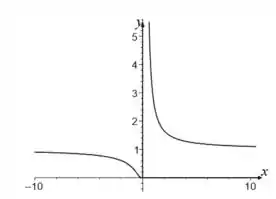
Resposta