Considere a curva:

Esboce o gráfico da curva determinando, caso existam: Assíntotas horizontais e verticais, intervalos de crescimento e decrescimento, pontos críticos, extremos relativos (locais), concavidades e pontos de inflexão.

Vamos determinar as assíntotas agora. As assíntotas verticais ocorrem nos pontos que não pertencem ao domínio. Como a função não tem restrições ao domínio, então não teremos assíntotas verticais.

Vamos para as assíntotas horizontais. Para calculá-las, vamos determinas os limites nos extremos:

Temos aqui uma indeterminação sacana, vamos tentar sair dela. Deixando o em evidência:

De maneira análoga:

Como o limite não existe, então não há assíntotas horizontais também!

Vamos determinar agora os intervalos de crescimento e decrescimento da função. Para tal, precisamos da derivada, então vamos derivar:

Precisamos determinar os pontos onde a derivada é maior ou menor que zero. Para tal, vamos determinar as raízes:

Então, temos que , para e e e . Então, a função é crescente para e e decrescente para .

Os pontos críticos ocorrem quando a derivada é zero ou não existe. Pela expressão da derivada:

Isso ocorre quando , já que teremos:

Que não existe. E , onde a derivada zera.

Vamos determinar agora os pontos de máximo e mínimo. Os pontos de máximo e mínimo ocorrem nos pontos críticos. Vimos no passo anterior, que e são os pontos críticos.

No passo , vimos que a derivada tem o mesmo sinal tanto à esquerda quanto à direita de , logo, esse ponto não é nem de máximo, nem de mínimo.

Da mesma forma, vimos que a derivada é negativa à esquerda de e positiva à direita de , logo, pelo teste da primeira derivada, esse é um ponto de mínimo.

Finalmente, para , a derivada é positiva à esquerda e negativa à direita e trata-se, portanto, de um ponto de máximo.

Vamos agora para a concavidade. Para tal, precisamos calcular a segunda derivada, então vamos derivar novamente:

Pela expressão, , para e para . Logo, a função é côncava para cima para e côncava para baixo para .

Por fim, os pontos de inflexão ocorrem quando a função troca de concavidade, o que acontece justamente em .

Ufa! Agora, usando os dados que obtivemos nos passos anteriores, chegamos ao gráfico: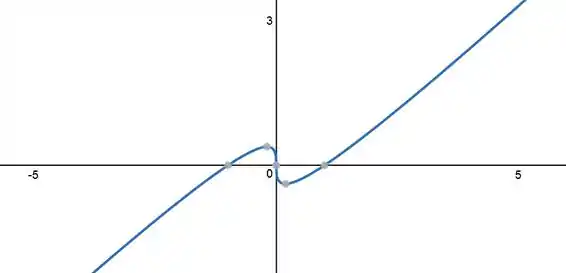

Os pontos em destaque são, da esquerda para à direta, o ponto da interseção com o eixo , o ponto de máximo em , o ponto de interseção, crítico e de inflexão em , os pontos de mínimo e, finalmente, a interseção .