A figura abaixo representa o gráfico de uma função .
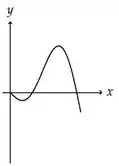
A figura que mais se aproxima do gráfico de uma primitiva de é:
a) 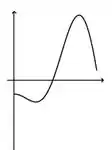
b) 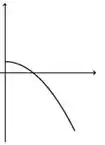
c) 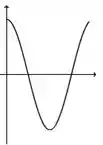
d) 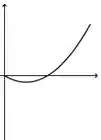
e) 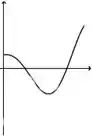
Passo 1
Vamos entender o que a gente tem e o que ele quer. Se uma função é primitiva de uma função , a gente pode dizer que:
E fazendo o caminho inverso:
Essa última informação é muito interessante! O que ele está dizendo no enunciado é que a gente tem o gráfico da derivada de uma função, e através dele, a gente quer achar que função é essa.
Passo 2
E quais são as correspondências entre esses gráficos? Onde o gráfico da derivada é positivo, nossa função precisa ser crescente.
E onde o gráfico da derivada é negativo, nossa função precisa ser decrescente.
Mas lembra que também podemos ver o sinal da derivada segunda de através do gráfico de sua derivada primeira.
Como? É só a gente vê onde o gráfico da derivada primeira é crescente ou decrescente. Porque com isso a gente vê o sinal de , que é o mesmo que ver o sinal de:
E com o sinal da derivada segunda de , podemos analisar sua concavidade.
Aí a gente pode até fazer duas tabelinhas com as informações que vamos usar


Bora lá!
Passo 3
Esse é o gráfico da nossa derivada
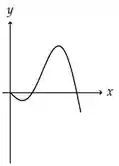
A gente vê que ele tem um intervalo negativo, depois um positivo e aí volta a ser negativo . De acordo com a nossa tabelinha:

Nossa função precisa ser decrescente, depois crescente e depois decrescente de novo.
Passo 4
Esse é o gráfico da nossa derivada . Vamos observar agora onde ele é crescente ou decrescente. Assim a gente avalia o sinal de .
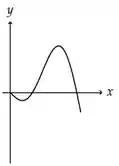
A gente vê que ele tem um intervalo decrescente, depois um crescente e aí volta a ser decrescente. De acordo com a nossa tabelinha:

Nossa função precisa ter concavidade para baixo, depois para cima e depois para baixo novamente.
Passo 5
De acordo com as informações que a gente reuniu, nossa função precisa começar sendo decrescente e com concavidade para baixo. E isso acontece em todas, menos na letra d.
Vimos também que nossa função precisa decrescer, depois crescer e aí voltar a decrescer de novo. A única que faz isso claramente é a da letra a.
Então essa vai ser a nossa resposta. 😊
Resposta
Letra a