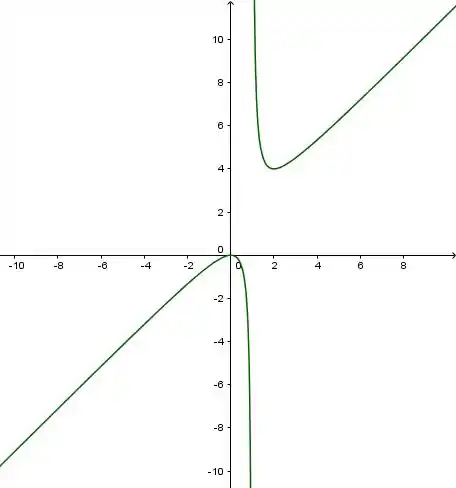
Considere a função dada por
- Encontre, caso existam, as assíntotas verticais e horizontais ao gráfico de .
- Determine os pontos críticos de , intervalos onde a função é crescente e onde a função é decrescente.
- Encontre os extremos relativos e absolutos de , caso existam.
- Determine os intervalos onde o gráfico da função possui concavidade voltada para cima e concavidade voltada para baixo.
- Esboce o gráfico da função .
Passo 1
(a)
Comecemos pelas assíntotas verticais!
Repare que:
Ou seja, na hora de calcular , vamos teruma divisão por zero!
é o único ponto causador de problema da função (não tem raiz quadrada nem logaritmo), portanto, o domínio da é:
Passo 2
Beleza, então é nossa candidatata a assíntota vertical. Vamos calcular os limites laterais nela:
Os limites explodiram pro infinito, então de fato é assíntota vertical da .
Passo 3
Agora vamos pras assíntotas horizontais.
Basta calcular os limites no infinito:
Usando a regra de l’Hôpital (nem precisaria mas assim é mais rápido), isso dá:
Da mesma forma, temos que:
Bem, os 2 limites foram pro infinito, então não tem nenhuma assíntota horizontal.
Passo 4
(b)
Essa questão toda quer nos levar até a letra (e), onde finalmente vamos esboçar o gráfico da função.
E pra isso temos que achar os pontos críticos da função. Diria que essa é talvez a etapa mais importante, porque com ela descobrimos onde a função cresce e onde ela decresce!

Enfim, vamos lá, derivando com a regra do quociente:
Passo 5
Ok, agora que temos a derivada vamos igualá-la a zero:
Deixando o em evidência no numerador:
Excelente! A função tem 2 pontos críticos, um em e outro em .
Passo 6
Agora temos que determinar os intervalos onde a função é crescente e onde a função é decrescente. E esses intervalos sobre os quais vamos nos debruçar (nossa que frase pedante) são:
Vamos montar uma tabelinha pra estudar o sinal da derivada nesses intervalos:
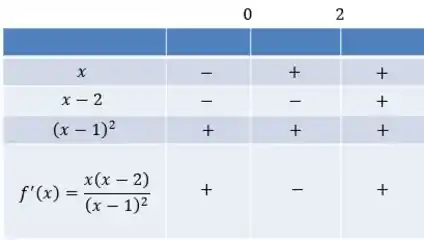
Daí concluímos que:
- é crescente no intervalo
- é decrescente no intervalo
Passo 7
(c)
Essa vai ser tranquila, já calculamos tudo que precisa!
Pelo teste da primeira derivada, é um ponto de máximo local, e é um ponto de mínimo local.
E vimos também lá atrás que
Ou seja, a função não tem extremos absolutos!
Passo 8
(d)
Suave, só precisamos calcular a segunda derivada e estudar o sinal dela. Lembrando que:
Derivando de novo, com a regra do quociente:
Deixando o em evidência no numerador:
Corta com o do denominador, e desenvolve o resto:
Daí vai cortar um monte de coisa e sobrar só:
Passo 9
Tranquilo de analisar o sinal disso, né?
Da mesma forma, temos que
Então concluímos que:
Passo 10
(e)
Show, agora “só” falta o esboço. Vamos fazer aquele resuminho maroto de todas as informações que descobrimos sobre a função ao longo da questão!
Sabemos que nesse intervalo a função é crescente e tem concavidade pra baixo. Também temos que:
Esse é um ponto de máximo local, e o valor da função nele é:
Nesse intervalo é decrescente, e tem concavidade voltada pra baixo. Vimos que:
Ou seja, a função decresce bem rápido nesse intervalo!
Sabemos que
E que é decrescente, com concavidade voltada pra cima nesse intervalo.
Ponto de mínimo local, e o valor de nele é:
A função é crescente, com concavidade voltada pra cima, e:
Passo 11
Aqui está o esboço!
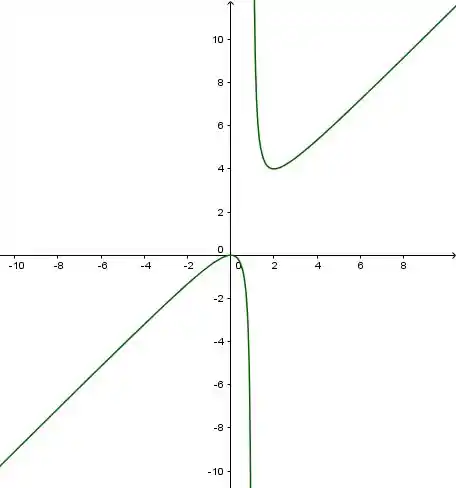
Resposta
(a)
Assíntota vertical:
Assíntota horizontal: não tem :/
(b)
Pontos críticos: e
é crescente no intervalo
é decrescente no intervalo
(c)
Extremos relativos: máximo local em , mínimo local em
Extremos absolutos: não tem...
(d)
Concavidade voltada pra baixo:
Concavidade voltada pra cima:
(e)